Free 모나드 패턴

Posted on July 3, 2020
  1. 비유하자면…
  2. Free 모나드 패턴의 목적
  3. Free 모나드
  4. Free 모나드 join
  5. Free 모나드 아이디어
  6. Free 모나드 패턴
  7. 진짜 펑크터를 넘기면 원하는 모나드 동작을 할까?
  8. MyMaybe
  9. MyReader

아래 목적을 이루기 위해 Free 모나드를 활용하는 패턴입니다. Free 모나드 자체가 아래 용도만을 위해 만들어진 건 아니지만 실용 코드에서는 아래 목적으로 사용하는 걸 자주 만납니다. (다른 용도로 쓰는 걸 아직 못 봤습니다.) Free 모나드만 단독으로 자세히 보려면 적당한 글이 아닙니다. Free 모나드를 이용해서 DSL을 구현하는 패턴을 다루는 글입니다. Free 모나드로 이렇게 긴 글을 쓰게 될 줄은 몰랐습니다. 아직 완전히 이해하지 못한 상태에서도 이런데, 이해가 끝나면 꽤나 긴 글이 될 것 같습니다.

2024년 12월 15일 추가) Free 모나드에 관한 정리를 새로 올렸습니다. Free 모나드가 뭔지 궁금하시면 새로 올린 글이 더 적당합니다.

비유하자면…

빈 상자들을 연결(바인딩) 가능하게 설계해 두고, 어떤 것(펑크터)이든 상자에 넣기만 하면, 연결 가능하니까 모나드라 우깁니다. 제 생각엔 겉 상자가 모나드지, 안에 들어 있는 건 여전히 모나드가 아니잖아… 란 생각이 들지만, 어쨌든 모나드라 부릅니다.

겉 모양으로 요약한다면, Free와 펑크터가 샌드위치처럼 교대로 쌓여져 있는 구조를 연결하는 모양입니다.

Free 모나드 패턴의 목적

Free 모나드가 아닌, 보통 Free 모나드 패턴이라 부르는 코드의 목적은 다음과 같습니다.

  Act1
  Act2
  Act3
  ...
  Done

이렇게 할 일을 직관적으로 코드에 표현하는게 목적입니다. (할 일을 명령형 프로그램 비슷하게 늘어 놓는게 목적입니다.)

Free 모나드

data Free f r = Free (f (Free f r)) | Pure r

instance Functor f => Functor (Free f) where
  fmap f (Pure x) = Pure (f x)
  fmap f (Free g) = Free (fmap f <$> g)  

instance (Functor f) => Monad (Free f) where
    return a = Pure a
    (Free x) >>= g = Free (fmap (>>= g) x) --(1) 
    (Pure r) >>= g = g r

바인드의 Pure와 매칭됐을 때 말고, Free와 매칭됐을 때를 직관적으로 해석해 보면,
Free 바인드가 하는 일은
Free ... (Free ...(Free ... Pure)) 이런 모양의 값에,
겹마다 있는 펑크터의 컨텍스트를 발현(fmap 실행)하고, (여기선 함수g를 실행하는게 아닙니다.)
Pure를 만나면 함수g를 적용하고 끝냅니다. 겹마다 있는 펑크터가 Maybe였다면 Nothing인지 검사하는 작업을 매 번 할테고, List였다면 안에 들어 있는 모든 엘리먼트에 각각 >>= g를 적용합니다. (※ 하지만, 대부분 예시를 보면 기존 펑크터를 이용하기보다, 단순히 안쪽으로 파고 들어가는 fmap을 가진 펑크터를 정의해서 활용합니다.)

(fmap (>>= g))를 이해하기 위해 다른 말로 정리해 보겠습니다.

Free의 바인드는 Free x >>= g = .........x.. 모양으로 유심히 보면 Free를 벗겨내고 있는 게 보입니다.
펑크터의 fmap은 펑크터를 벗겨 냅니다. (다른 말로, 펑크터 안으로 파고 들어갑니다.)

Free (펑크터 (Free (펑크터 (Free 타입인 Pure ... )))) 이런 구조가 싸고 있는 가장 안쪽 값에 도달하려면
Free를 벗겨내기 위해 Free 바인드, 그 다음
펑크터를 벗겨내기 위해 펑크터의 fmap, 그 다음
Free를 벗겨내기 위해 Free 바인드, 그 다음
펑크터를 벗겨내기 위해 펑크터의 fmap, 그 다음
Pure를 만나 함수 적용.

이런 동작을 위해 Free 바인드는 펑크터 fmap을 부르고, fmap은 Free 바인드를 부르는 걸 반복합니다.

※ 이런 구조를 읽는데서 그치는 게 아니라, 이런 구조를 떠올릴 수 있는 지식을 쌓으려고 노력 중입니다.
“모나드 생성자를 벗겨내려면 바인드를, 펑크터 생성자를 벗겨 내려면 fmap을 적용한다”
라고 읽을 수 있게 머릿속에서 한 번 정리해 두면 좋을 것 같습니다.

-- (1)번의 오른 쪽 Free의 안 쪽 것만 보면
(fmap (>>= g) x)
-- x는 왼쪽 Free x로 받은 것에서 Free를 떼어낸 것

위의 x는 펑크터입니다. x는 f (Free f r) 입니다. 하스켈은 펑크터f 인스턴스의 fmap을 선택합니다. 펑크터 안에 들어 있는 값 Free f r에 다시 >>= g를 적용합니다.

-- Free x는 Free (f (Free f r)) 값이거나, Pure r 값
-- Free값일 때 x 와 (f (Free f r)) 이 매칭
(Free f r) >>= g

여기의 바인드는 다시 Free를 받으므로, 하스켈은 다시 Free 바인드를 선택합니다. Free값을 받으면 안 쪽 값에 다시 바인드를 먹입니다. 언제까지? Pure값을 만날 때까지 계속합니다. 다른 모나드들 모두 해당 모나드 타입을 돌려주는 함수를 인자로 받듯이, Free 모나드의 바인드가 받는 g는 Free 타입 값을 리턴하는 함수입니다.

일단 재귀가 등장하면 생각이 복잡해집니다. 재귀가 무한대로 가면 더욱 따라가기가 불편해집니다. 재귀를 보면 딱 한 단계만 진행하거나, 어떤 조건하에서 끝난다는 걸 알고 읽으면 도움이 됩니다. 여기서는 Pure를 만나면 끝납니다.

위 바인드를 정리해 보면 (Free타입 A)와 (Free타입 B를 돌려주는 함수)가 만나면, 컨텍스트는 계속 발현(fmap)될 수 있는 모양을 유지하며 A의 가장 안쪽에 B를 붙이는 작업을 합니다.

-- 실제 코드는 모두 Free지만, 설명하기 위해 편의상 Free에 번호를 붙이겠습니다.
Free1..(Free2..(Pure..)) >>= (\_->Free3..(Free4..(Pure..)))

-- 결과는
Free1..(Free2..(Free3..(Free4..(Pure..))))

대부분 Free(..(Free..))와 같은 값을 만나고, 여기에 바인드로 (\_ -> Free ...) 함수를 적용하면 Free가 몇 번 감싸져 있든 안쪽까지 들어가 Pure r에 도달해서 r에 함수를 적용하므로 가장 안쪽에 이어 붙이는 효과가 납니다. 적용하는 함수는 리턴 타입이 Free 타입이니, 결과는 Free 속에 Free를 넣은 형태가 됩니다.

어떤 펑크터가 됐든 Free로 감싸서 Free타입으로 만들면 .. 이라 표시된 자리에 펑크터 값이 들어갑니다.

Free 모나드 join

모나드가 하는 일이 눈에 잘 들어오지 않을 때는 join으로 effect를 합성하는데 어떤 정보를 남기는지 보면 도움이 됩니다.

※ join 구현 참고 - 모나드, 같음 - m (m a)와 m a는 얼마나 다를까?

Free 모나드의 join 동작을 보면

-- x는 Free f r 타입입니다.
join (Pure x) = (Pure x) >>= id
              -- join이 m(m a)를 받으므로 x는 Free f r타입입니다.
              = id x
              = x -- Pure 하나만 벗긴 것
join (Free (f (Pure x))) = (Free (f (Pure x))) >>= id 
                         = Free (fmap (>>= id) (f (Pure x)))
                         = Free (f (Pure x >>= id))
                         = Free (f (id x)) 
                         = Free (f x) -- join이 m(m a)를 받으므로 x는 Free f r 타입입니다.

-- join에 Free (Free ..)을 넘길 때와 join에 Free (Pure ...)를 넘길 때
join (Free (f (Pure      (Free(f (Pure x)))      ))) = Free (f (Free (f (Pure x))))
join (Free (f (Pure      (Pure x)                ))) = Free (f (Pure x))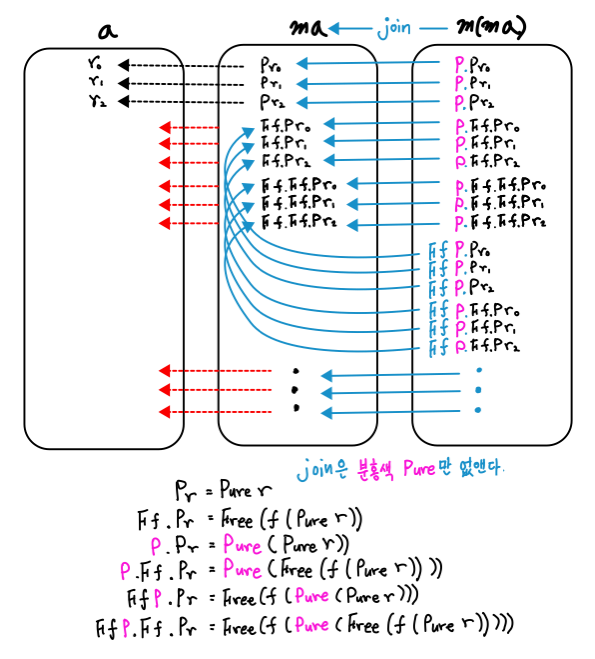
Free 모나드 join

이해하기 좋게 그리기가 쉽지 않습니다. 목표는 펑크터 f가 모두 살아 남게 합성해야 합니다.

join (   Free (f (Pure (Free (f (Pure r)))))   ) -- :: m (m a)
=        Free (f (Free (f (Pure r))))            -- :: m a
-- 중간에 Pure 하나만 뺀 모양입니다.

Free (f (Free (f ...))) 모양은 유지하면서 사이 사이에 끼어 있는 펑크터들을 순서에 맞게 계속 보존합니다.

Free 모나드 아이디어

모나드를 엮을 때 컨텍스트가 발현 되는 곳만 보면, 모나드가 아니라 Functor의 fmap이 담당합니다. 이렇게 동작한 액션을 다음 액션과 물릴 때 모나드가 나서게 됩니다. 그렇다면, 엮는 동작만 하는 코드를 따로 추상화 해놓으면, Functor를 손쉽게 모나드로 만들 수 있지 않을까 했는데!, 그건 아니었습니다!!

바인드가 fmap을 동작시켜 컨텍스트가 발현되면서 묶는 작업을 하니, 어떤 펑크터든 엮을 수 있을 줄 알았는데, 지금 이 글을 쓰기 위해 Reader 모나드를 Free로 구현하다 보니, 아무 펑크터나 받을 수 있는 게 아니었습니다. Free 모나드의 바인드가 하는 일은 범용 join이 아닙니다.

... fmap (>>=g) ...

g를 적용하는게 아니라, 바인드로 g를 연결하는 걸 넘겨 g의 실제 적용은 계속 뒤로 밀려납니다.

샌드위치처럼 Free와 펑크터를 몇겹으로 붙여 놓은 것들끼리 연결하는 게 주요 동작입니다. 왜 펑크터를 몇 겹으로 해 놀 필요가 있었을까요? Free 모나드 패턴처럼 하기 위해서였다면 (작업 단계를 나열하는 구조를 원했다면) 아래처럼

[펑크터, 펑크터, 펑크터...]

이렇게 리스트로 하고, 하나씩 꺼내서 인터프리팅하면 되지 않았을까요?
리스트도 모듈 구현도 가능하고, 차이점은 do구문을 쓴 Free모나드가 깔끔한 외관을 지닌 것 정도 말고 뭐가 있을까요?

-- 모듈식으로 한다면
[펑크터, 펑크터, 펑크터...] <> [펑크터, 펑크터] <> [펑크터, 펑크터, 펑크터...]

Free 모나드로 구현한 DSL 패턴을 리스트로도 구현할 수 있을 것 같은데, 왜 특별히 Free 모나드를 만들었을까요?

참고 - Overcoming Software - What does Free buy us?

그 이유는, 아래 예를 든 Act같이 단순한 경우는 리스트로 구현해도 되지만, DSL의 명령어들이 리턴값이 있을 경우 단순 리스트로 구현할 수 없습니다. 달리 표현하면, 리스트에선 먼저 실행한 명령의 결과를 가져와 그 다음 명령에게 줘야 할 때 어떻게 할 방법이 없습니다. (인터프리터 단계에서 State 모나드등을 써서 해결할 수 있을 것 같긴 합니다.) 다음 명령어에게 결과를 넘기기 위해 타입에 next 자리를 넣어 이어지는 명령에 결과값을 넘기도록 할 수 있습니다. 그런데 이렇게 next 자리를 타입에 만들면 더 이상 리스트로 시퀀싱을 표현할 수 없습니다. 리스트의 원소는 서로 어떤 영향도 주지 않는 독립된 요소입니다.

CPS에서도 다음 이어지는 함수를 넣는 테크닉을 썼는데, 여기와 CPS의 다른 점은? 여기선 함수만 써주는게 아니라, 다음 할 일을 나타내는 단순한 태그를 써주거나, 이전 명령의 결과값이 다음 명령어로 넘어가야 할 때는 함수 형태를 쓰기도 합니다.

사실 리스트 값은 Cons x1 (Cons x2 (Cons x3 []))의 편의 표현입니다. Free값 Free (Functor (Free Functor (Free (Functor (Pure ())))))과 많이 닮아 보이지 않나요? 펑크터로 (,)를 넘기면 Free로 리스트를 만들 수도 있습니다. 둘의 차이는 Free는 어떤 펑크터든 받아서 구조를 만들 수 있는 상태고, 리스트는 이미 정해진 펑크터를 받아 구조가 완성된 상태입니다.

품는nested 구조 자체야 수 많은 곳에 쓰이는데, 이해가 까다로운 게 어찌 보면 품는 구조가 익숙하지 않아 그럴 수도 있겠습니다. 말을 하다 보니, 품는 구조에 익숙하지 않다는 말은, 함수형에 익숙하지 않다와 거의 동의어처럼 느껴집니다.

람다 대수의 기본 틀이 품는 구조입니다. 이 걸 그대로 가져온 게 함수형 프로그래밍입니다. 데이터 구조를 만들 때 첫 번째로 해야 하는, 무의식 중에 자연히 써먹어야 하는 틀인데 전 그렇지 못 해 계속 훈련 중입니다. 참고 - 품고 품기

Free 모나드 패턴

여기 예시는 단순화해서 Free 모나드의 장점이 모두 드러나진 않지만, 개념을 이해하는데는 부족하지 않아 보입니다.

-- Act1하고 Act2하는 작업이든...
-- Act1하고 Act2하고 Act1하는 작업이든...
-- Act가 몇 번이 반복되든 모두 같은 타입으로 만드는 방법은 재귀를 이용하면 됩니다.
-- 리스트가 재귀로 선언 되어 [],[0,1],[3,4,...] 이런 모양들을 모두 
-- 같은 리스트 타입으로 볼 수 있는 것과 비슷합니다. (각주 [1] 참고)
-- 나중에 Free타입이 들어 올 자리 next를 추가합니다.
-- Act 타입 단독으로 재귀적으로 표현되는게 아니라, Free로 감쌀 때 next를 이용해 재귀적으로 표현됩니다. 
data Act next = Act1 next | Act2 next | Done

-- Free 정의를 보면 functor를 받게 되어있는데, 바인드 안 쪽을 보면 fmap을 부릅니다. 
-- 펑크터로 만들어야 한다는 얘깁니다.
instance Functor Act where
  fmap f (Act1 next) = Act1 (f next)
  fmap f (Act2 next) = Act2 (f next)
  fmap f Done = Done

-- 위 Act 타입을 Free로 감싸놓습니다.
act1 = Free (Act1 (Pure ()))
act2 = Free (Act2 (Pure ()))
done = Free (Done          )

※ 각주 데이터의 재귀 참고1

이제 act1, act2, act2, act1, act2, done 순서로 작업을 해야 된다면

Free(Act1 (Free(Act2 (Free(Act2 (Free(Act1 (Free(Act2 (Free Done))))))))))

이렇게 쓰면 됩니다. 작업을 연결해서 표시할 수 있게 되긴 했는데 좀 복잡합니다. 하지만 Free는 모나드입니다! 바인드가 잘 정의되어 있어 이렇게 쓰지 않고, 이들을 모두 바인드로 연결해도 똑같은 코드입니다.

act1 >>= \_ -> act2 >>= \_ -> act2 >>= \_ -> act1 >>= \_ -> act2 >>= \_ -> done

Free는 모나드이므로 do로 바인드를 가리면

do
  act1
  act2
  act2
  act1
  act2
  done

이렇게 예쁘게 적을 수 있습니다. 더 나아가

actProc1 = do
  act1
  act2
  done

actProc2 = do
  act2
  act1
  act2
  done

acts = do
  actProc1
  actProc2
  done

이렇게 적을 수도 있습니다. 딱 봐도 DSL(Domain Specific Language)을 만드는데 유용해 보이지 않나요? 실제로 DSL을 만들기 위해 많이 씁니다. (사실, 아직까지 DSL 말고 쓰는 경우는 보지 못했습니다.)

이론적인 모나드의 목적이라기보다, 하스켈에 있는 모든 모나드의 목적은 컨텍스트를 끌고 다니며 품고 품는 구조로 만드는 것입니다. 이렇게 만들고 나면 이어지는 람다 함수의 헤드에 각 단계마다의 실행 결과를 넣어 둘 수 있는 장점이 생깁니다.

참고 - 모나드 체인이 목표하는 코드 모양과 실행 순서

do
  r1 <- act1
  r2 <- act2
  ...

이렇게 연결된 구조만 만들어 작업 명세서만 만들어 놓고, 이 명세서를 보고 실제 동작을 하는 코드를 따로 만듭니다. 이런 코드를 보통 인터프리터라고 부릅니다.

-- 인터프리터 예시
showFree :: Free Act () -> String
showFree (Free (Act1 next)) = "act1 " ++ showFree next
showFree (Free (Act2 next)) = "act2 " ++ showFree next
showFree (Free (Done     )) = "done "

> showFree acts
"act1 act2 act2 act1 act2 done "

-- 바인드 구문과 함수 연결 표현이 같은 구문인지 확인
-- 아래 구문이 가장 확실한 프리모나드 동작 설명이 아닐까요
> showFree (Free(Act1 (Free(Act2 (Free(Act2 (Free(Act1 (Free(Act2 (Free Done)))))))))))
"act1 act2 act2 act1 act2 done "

정리하면,

  1. 작업을, Free 타입이 들어올 자리를 가진 대수 타입으로 만들고,
  2. 이 타입을 펑크터로 만들고,
  3. 작업과 매칭되는 Free 타입을 만들어
  4. Free 모나드의 do 구문으로 작업 목록을 만들어 놓으면
  5. 나중에 인터프리터에 넘겨 작업 목록을 실행한다.

가 “Free 모나드 패턴”입니다.

진짜 펑크터를 넘기면 원하는 모나드 동작을 할까?

펑크터를 받으면 공짜로Free 모나드를 만들어 준다기에, 그럼 기존 모나드들도 Free로 구현할 수 있는 한 번 시도해 봤습니다.
결론부터 말하면, Reader를 정의하기 위해 펑크터(fmap)를 잘 정의하고, Free에 넣는다고 Reader 모나드가 되지 않습니다. 다른 형태의 바인딩이 가능한 모나드가 될 뿐입니다. Free 모노이드2와 비슷하게, 바인딩이 되는 구조(틀)를 만들어 놓고, 그 안에 밀어 넣으면서 “바인딩이 되니 모나드가 된거야”라고 말할 뿐, 원하는 모나드가 되진 않습니다. 공짜를 뜻하는 Free가 아니라, 모나드 이름이 Free인 모나드라고 해야 할 것 같습니다.

공짜로? 모나드 되기. 단 Free 모나드만 될 수 있습니다.

MyMaybe

Maybe와 같은 MyMaybe를 정의하는데, 펑크터까지만 만들어 두고, Free를 씌워서 모나드 동작을 하는지 살펴봤습니다.

참고 : Maybe 모나드 정의

return :: a -> Maybe a
return x  = Just x

(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
(>>=) m g = case m of
                Nothing -> Nothing
                Just x  -> g x
import Data.Functor
import Control.Monad.Free
data MyMaybe a = MyJust a | MyNothing 
instance Functor MyMaybe where
    fmap f (MyJust x) = MyJust ( f x )
    fmap f MyNothing = MyNothing

exFuncPositive :: Int -> Free MyMaybe Int
exFuncPositive x | x > 0 = Pure x
                  | otherwise = Free MyNothing

exFuncEven :: Int -> Free MyMaybe Int
exFuncEven x | x `mod` 2 == 0 = Pure x 
              | otherwise = Free MyNothing

exFunc3x :: Int -> Free MyMaybe Int
exFunc3x x | x `mod` 3 == 0 = Pure x
            | otherwise = Free MyNothing

func :: Int -> Free MyMaybe Int
func x = do -- 모나드 동작
    v1 <- exFuncPositive x
    v2 <- exFuncEven v1
    exFunc3x v2
    
main :: IO ()
main = loop
    where  
      loop = do
        a <- getLine
        case func (read a) of
            (Pure x) -> print x
            Free MyNothing -> putStrLn "MyNothing"
            _ -> putStrLn "?"
        loop

따로 예외 처리는 안했습니다. 2의 배수, 3의 배수, 2와 3의 공배수를 입력해 보세요. func 함수가 Maybe 모나드와 같은 동작을 합니다. 타입과 값을 써 줄 때 Free의 생성자를 계속 끌고 다니는 불편함은 있지만 모나드를 얻긴 했습니다. 원하는 동작을 하니, 펑크터만 잘 만들어 넣으면 원하는 모나드가 될 것처럼 오해할 수 있습니다.

위에 필터 함수들의 통과 값이 Free (Just (Pure x))가 아니라 Pure x인게 밟힙니다. 아래 다른 예를 한 번 더 보겠습니다.

import Data.Functor
import Control.Monad.Free
data MyMaybe a = MyJust a | MyNothing deriving Show
instance Functor MyMaybe where
  fmap f (MyJust a) = MyJust (f a)
  fmap f MyNothing = MyNothing

act1 :: Free MyMaybe String
act1 = Free(MyJust(Free(MyNothing))) -- MyJust
-- act1 = Free MyNothing

act2 :: Free MyMaybe String
act2 = Free MyNothing -- MyNothing

func :: Free MyMaybe String
func = do
    act1
    act2

interpreter :: Free MyMaybe String -> String
interpreter fr = case fr of
     Free (MyJust x) -> "Just" <> interpreter x
     Free MyNothing -> "Nothing"
     Pure e -> "Pure "

main :: IO ()
main = putStrLn $ interpreter func

MyNothing 값을 엮었으니 func는 MyMaybe의 컨텍스트가 작동해서 모두 합친 결과는 MyNothing이 나올거라 예측했다면 Free 모나드를 아직 잘 못 이해한 겁니다. 결과값은 Just Nothing입니다. func값은 아래와 같습니다.

-- 손대지 않은 act1 그대로 값입니다. act2와 바인딩하는데 
-- fmap이 MyNothing을 만나 더 이상 바인딩을 진행하지 않습니다.
-- 바인딩할 때 fmap 컨텍스트가 작동해서 바인딩을 끊어버렸으니 
-- MyMaybe는 역할을 하긴 했는데 그렇다고 전체 결과가 
-- MyNothing으로 바뀌는 건 아닙니다. 
-- MyNothing을 만나기 전 통과했던 MyJust들은 모두
-- 그대로 살아서 Free로 쌓여 있는 상태입니다.
Free(MyJust(Free(MyNothing)))

더 이상의 reduce가 필요 없습니다. 이대로가 값이니, 첫 번째 Free가 감싸고 있는 것은 그냥 MyJust이고, 두 번째 안 쪽 Free가 감싸고 있는 건 변함없이 MyNothing입니다. 저도 한동안 Free가 컨텍스트를 발현시키며 엮어 준다고 생각했습니다. 하지만 Free값은 이미 엮여저 있는 상태고, 엮여져 있는 모양은 변하는게 아닙니다. 물론, 다른 Free와 바인딩할 때 중간에 Nothing을 만나면 더 이상 바인딩 하지 않습니다. Maybe의 컨텍스트가 발현되긴 했지만, Maybe모나드처럼 결과가 단순 Nothing이 되는게 아니라, 그 때까지 바인딩한 결과는 그대로 살아 있게됩니다. Free 바인드는 엮은 것 속에 넣어 이어서 엮어 주는 역할만 합니다. 그럼 첫 번째 MyMaybe의 예는 어떻게 해석할까요?

Pure x를 만나면 쓰이는 바인드는 (Pure r) >>= g = g r 로 r을 바로 꺼내 g를 바로 적용합니다. 그래서 Maybe와 우연히 같은 동작을 합니다.

정리하면, 펑크터 단독으로 겹겹이 싸 놓으면 다른 펑크터와 연결할 수 없지만, Free모나드라는 칸막이를 중간 중간 넣어 겹겹이 싸 놓으면 다른 겹겹으로 싸 놓은 펑크터와 연결이 가능해집니다. 이미 엮여 있는 값에서 펑크터의 컨텍스트가 순차적으로 드러나는 건 아닙니다. 이 걸 다른 것과 바인딩하게 되면 하나 하나 벗겨 내면서, 그 때부터 컨텍스트가 드러날 순 있는데, 대부분 Free 모나드 패턴에 쓰이는 펑크터의 fmap은 별다른 컨텍스트 없이 안으로 파고드는 작업만 합니다. 굳이 겹칠 때마다 컨텍스트가 의미가 있다면 바인딩할 때 발현 되긴 합니다.

정리하면, 모나드를 얻긴 하지만, 생각했던 펑크터 컨텍스트를 끌고 다니며 연결하는 모나드가 아니라 “Free 모나드”를 얻을 뿐입니다.

MyReader

이번엔 위처럼 최종 활용되는 코드로 살펴보는게 아닌, 실제 바인딩을 따라가 봤습니다.

newtype MyReader e a = MyReader { runMyReader :: e -> a }
instance Functor (MyReader e) where
  fmap f mr = MyReader (\r -> f (runMyReader mr r)) ---- (가)

그럼, 이런 fmap을 가진 펑크터 MyReader를 Free로 감싸 놓으면 어떤 모나드 역할을 할 수 있는지 보겠습니다.

※ 함수란 앞으로 일어날 일을 준비하는 겁니다. 인자를 받을 자리(매개 변수)가 있다는 얘기는, 언젠가 미래에 값을 받겠다는 얘기입니다. 이 값이 들어오기 전까지는 준비 상태일 뿐입니다. 분명 모호하게 이해되는데는 다 이유가 있다고 생각합니다. 이유를 찾는 중인데, 함수에 대한 이해가 부족해서 그런 건 아닐까 하고, 함수를 이런식으로 해석하고 더 읽어 보겠습니다.

Reader의 컨텍스트는 외부에서 r을 받아 함수를 실행한 후 f를 적용하는 식으로 reduce 해서 생각하는 게 아니라 Reader의 컨텍스트는 외부에서 r을 받아 함수를 실행한 후 f를 적용할 준비 상태로 만드는 겁니다.

data Free f r = Free (f (Free f r)) | Pure r
--    T   T T     V   T    T  T T      V   T
-- 나중에 값에서는 
--                V   V    V  V V      V   V 
-- T는 타입 생성자
-- V는 값 생성자

                Free (Just  (Free Just 1)) -- 값
                Free (Maybe (Free Maybe Int))  -- 타입? 아닙니다. 
                -- 이 것의 타입은 Free Maybe Int 타입입니다.
                -- data 선언할 때 =의 오른쪽은 타입도 아니고, 값도 아닙니다.
                -- "값을 만드는 방법"입니다.

Free를 모나드 인스턴스로 만드는 정의를 보면, 여기 쓰인 f는 펑크터란 제약이 있습니다. 펑크터 인스턴스의 키로 쓰일 타입은 * -> * 카인드입니다. 여기서는 MyReader e입니다. Free의 바인드를 풀어 보면 - 참고 타입 생성자와 값 생성자 혼동3

Free x >>= f = Free (fmap (>>= f) x)
Pure r >>= f = g r

Free 타입 값의 (타입이 아니라) 모양은 다음처럼 생겼습니다.
(f가 fmap정의에 있는 것과 혼동을 주니 functor로 바꿨습니다.)

Free x = Free (functor (Free (functor (Pure r))))

여기서 functor가 MyReader e이란 말은 Free로 감싼 타입은 Free (MyReader e) a 타입이란 말입니다. 이 건 값이 아니라 타입이고, 값의 모양은 다음처럼 될 겁니다. Free f r 에서 f에는 MyReader타입의 값 생성자 MyReader가, r에는 MyReader가 e -> a를 받으니, e -> a 함수가 들어갑니다. 좀 더 힌트를 읽어내면, Free로 묶으려면 결과 타입 a로는 Free ... 타입이 들어가니, e -> Free ... 타입 함수여야 합니다. 검증 필요

※ e -> a 형태가 되어야 하는다는게 불편한 분은 Free 정의를 다시 째려 보면 이해가 갑니다. 애당초 Free 정의에서 f는 인자 하나를 받는 펑크터라 되어 있는데 f (Free f r)이므로 (Free f r)은 f가 받을 수 있는 타입이어야 합니다. 아무 펑크터나 올 수 있는게 아니라, Free를 받을 수 있는 펑크터만 올 수 있습니다. 보통은 폴리모픽으로 열려 있는 펑크터들이 들어 옵니다. 위의 예에서 보면 data Act next = ...에서 next 가 폴리모픽으로 열려 있는 부분입니다. MyReader e 펑크터는 Free를 받아야만 Free 모나드로 감쌀 수 있습니다. 일단 타입이 지정이니 Reader 모나드와 같은 동작을 하게는 못 만들 것 같습니다.

2022-7-27 추가
하스켈에서 보통 다루는 펑크터는 모두 폴리모픽 타입 변수를 가집니다. 예를 들어 Maybe Int가 아니라 Maybe a입니다. 이게 항상 그런지는 확정해서 얘기하기엔 지식이 부족합니다. 만일, 항상 폴리모픽한 경우만 펑크터로 분류한다면, 모든 펑크터는 Free모나드로 감싸 모나드로 만들 수 있습니다.

-- Free (MyReader a) a 타입의 값은 다음과 같은 모양입니다.
Free (functor값생성자 (Free (functor값생성자 (Pure (Free를 리턴하는 함수)))))

Free (MyReader (\e -> Pure e)) -- (나)
Free (MyReader (\e -> Free (MyReader (\e -> Pure e))))
...

이렇게 나올 수 있는 값 모양 중, 간단한 (나)로 바인드 동작을 살펴 보겠습니다. (Free를 받을 수 있는 모나드로 가정해 보겠습니다.)

-- 바인드 동작 결과를 보기 위해 같은 생성자들은 번호를 붙였습니다.
Free1 (MyReader1 (\e -> Pure1 e)) >>= (\_ -> Free2 (MyReader2 (\e -> Pure2 e)))
= Free (fmap (>>= (\_ -> Free2 (MyReader2 (\e -> Pure2 e)))) -- >>=를 또 가져가고 있습니다.
                                                             -- 안 쪽에서 조건이 맞으면 또
                                                             -- fmap을 실행하기 위해서입니다.

             (MyReader1 (\e -> Pure1 e)))
-- fmap은 MyReader의 것이 작동합니다.
= Free ( MyReader (\r ->  (>>= (\_ -> Free2 (MyReader2 (\e -> Pure2 e))))   
                          (runMyReader (MyReader1 (\e -> Pure1 e)) r) -- MyReader 컨텍스트 발현!
                  )
       )
= Free ( MyReader (\r -> (runMyReader (MyReader1 (\e -> Pure1 e)) r) -- 첫번째 MyReader로 싸
                         >>= (\_ -> Free2 (MyReader2 (\e -> Pure2 e)))
                  )
       ) 
-- 코드를 읽으면서 이해하려고 할 때, 여기서부터는 
-- Free와 MyReader를 벗기면서 r을 넣어주지 않는한 reduce는 어렵습니다.
-- Free를 벗겨내는 인터프리터를 적용하고, runMyReader를 적용했다고 가정하면,
= Pure1 r ----- (다)
  >>= (\_ -> Free2 (MyReader2 (\e -> Pure2 e)))
-- 바인드는 Pure와 매칭되는 Free의 바인드가 작동합니다.
-- 만일 Free와 매칭되었다면, 또 fmap이 돌아 컨텍스트가 발현되었을 겁니다. 
= (\_ -> Free2 (MyReader2 (\e -> Pure2 e))) r ---- (라)
= Free2 (MyReader2 (\e -> Pure2 e)) -- 최종 결과값은 Free 값입니다.

A >>= B 바인드 동작은 A도 r을 받아 작업하고, B도 r을 받아 작업하게 하는게 Reader 모나드의 컨텍스트입니다. (다)에서 r을 적용하고, (라)에서 r을 적용하는게 보이긴 합니다.

정리하면, runMyReader는 fmap에서 작동합니다. Free는 fmap만 부르면서 품고 품도록(nested되도록) 엮는 역할만 합니다.

뭔가 복잡하게 풀어 헤쳐놔서 분명 어디선가 오류가 있을 것 같습니다. 진짜로 Free가 아무 펑크터나 모나드로 만들어 주는지 궁금해서 따라가 봤는데, 제대로 따라 간건지 의심이 듭니다.

리스트는 튜플 펑크터를 쓴 Free 모나드이니, 리스트에서 보이는 특징 대부분이 Free 모나드의 특징과 겹치기도 합니다. 하스켈을 공부하다 보면 한가지 개념이 이해에 도달할 때 쯤, 이게 만물의 근원처럼 느껴질 때가 있습니다. 모나드를 공부하다 보니 모든 함수가 모나드로 결론나고, Free를 공부하다 보니, 리스트도 Free모나드로 결론이 납니다. 정말 천재가 만들어서 그런건지, 세상의 이치인지 묘한 개념들이 한 쪽 으로 모이게 되어, 알고나면 단순한 언어처럼 느껴지고 왜 이런 단순함이 그리 어려웠을까 생각 해보게 되는 언어입니다.

참고 How do I implement Reader using free monads? - stackoverflow

2022-7-27 추가
하스켈 학교 디스코드에 제가 올렸던 글을 정리했습니다.

Reader로 만들기 위한 인터프리터

import Control.Monad.Free

newtype MyReader e a = MyReader { runMyReader :: e -> a }

-- 펑크터까지만 인스턴스를 만들고, 그 다음 인터프리터 정의
instance Functor (MyReader e) where
  fmap f mr = MyReader (\r -> f (runMyReader mr r))

-- 인터프리터
interp :: Free (MyReader e) a -> e -> a
interp (Free f) e = interp (runMyReader f e) e
interp (Pure r) _ = r
> interp (Free (MyReader (\e -> Pure (1 + e)))) 1
2
> interp (   Free (MyReader (\e -> Pure (1 + e))) >>= \r2 -> Free (MyReader (\e -> Pure (r2 + 2 + e)))    ) 1
5

MyReader와 interp의 조합으로 Reader모나드 동작을 할 수 있습니다. interp에서 Reader모나드의 join이 할 일을 하고 있습니다.

-- Reader 모나드의 join
join ((->) mma) = \e -> (((->) mma) e) e

요약

(State0, State1, State2, State3 다 같은 State 타입인데, 구분하기 위해 편의상 숫자를 붙였습니다. Free도 마찬가지입니다.)

State 모나드
(바인드에 이펙트를 합치는 작업이 있는 모나드의 예)

((State0 `이펙트 합쳐 새State 만들기` State1생성)
         `이펙트 합쳐 새State 만들기` State2생성)
         `이펙트 합쳐 새State 만들기` State3생성

별도의 인터프리터가 필요하지 않고, 그 때 그 때 생성된 이펙트들을 합칩니다.

Free 모나드

((Free0 `그냥 연결` Free1생성)
        `그냥 연결` Free2생성)
        `그냥 연결` Free3생성

이렇게 해놓으면, 그냥 연결은 말 그대로 아무 작업도 안하고 그냥 연결만 해 둡니다. 나중에 인터프리터에서 Free를 벗기면서 어떻게 이펙트 합치기를 할지 결정 합니다. 어떤 펑크터든 Free로 감싸 놓으면, Free의 바인드를 이용해 ((...functor...) ...functor...) ...functor... 모양으로 만들어 둘 수 있습니다. 리스트가 뭘 담든 상관 안하듯, Free도 어떤 펑크터를 담는지 신경쓰지 않습니다.

Freer모나드

Free는 펑크터를 받아 모나드로 만드는데, 펑크터가 아닌 아무 Type -> Type을 받아 모나드로 만드는 Freer도 있습니다.(끝에 r이 있습니다.) 둘 차이는,

free : 작업을 엮으면서, 이펙트는 발생하는데, 합치는 건 나중에 인터프리터가 알아서 해
freer: 작업을 엮으면서, 무슨 이펙트를 발생하게 할지도 나중에 인터프리터가 알아서 하고, 합치는 것도 인터프리터가 알아서 해

어차피 나중에 이펙트를 합치는 “추가 작업”을 한다면, 이펙트 생성조차도 나중에 맡기는 게 더 일반적일 수 있겠다는 생각이 듭니다. Freer은 공부를 좀 더 한 후에 따로 글을 올려야 할 것 같습니다.

@todo: F-algebra를 이용한 설명 추가

  1. 함수의 재귀와 데이터의 재귀 함수의 재귀는 함수안에서 함수를 부르고, 부른 함수에서 또 함수를 부르는데, 데이터 재귀는 그런 뜻이 아닙니다. 함수 재귀는 한 번 실행되기 시작하면 끝나는 조건을 만나기 전에는 계속 반복 실행하는데, 데이터 재귀는 실행의 개념이 아닙니다.

    List a = Empty | Con a (List a)

    는 다음과 같은 형태가 될 수 있다는 뜻이지, 데이터 생성자 Con안에서 타입 생성자 List를 만났다고 또 “실행”을 하는게 아닙니다.

    Con a (Empty)
Con a (Con a (Empty))
Con a (Con a (Con a (Empty)))
...

    이런 모양 모두 리스트 타입이 될 수 있다는 뜻입니다. 데이터 선언 자체에는 반드시 Empty 값으로 끝난다는 제약은 없지만, 실제 코드에서 의미있는 값들은 대부분 마감되는 형태로 나타납니다. (Lazy를 이용해서 무한 반복되는 모양이 나올 때는 마감 여부를 알 필요가 없고, 앞에 몇 개만 쓴다든지 하는 경우가 있긴 있습니다.)

    데이터 재귀를 만나면 머릿속에서 무한 “호출”을 하지 마시고, 그런 “모양이 올 수도 있다”라고 해석하면 됩니다.↩︎

  2. Free의 속 뜻
    같은 뜻으로 쓰인 Free 모노이드를 보면 이해하는데 도움이 됩니다.
    리스트를 Free 모노이드라 부릅니다. 영어 번역으론 타입을 받으면 Free 모노이드를 돌려주는 구조라 되어 있는데, 이런 설명식 문장으로 의사 소통이 귀찮은지 그냥 리스트를 Free 모노이드라 부르기도 합니다. 엄밀히 말하면 타입을 모노이드로 만드는 툴이 리스트이고, 이렇게 별 노력없이 만들어진 모노이드를 Free 모노이드라 부릅니다.

    This structure gives you a “free” monoid for a given type.

    어떤 타입이 들어있는 리스트이든, 리스트로 만들면 모노이드가 됩니다. 리스트가 무슨 매직을 부려 이렇게 할까요? 보통 “어떤 타입이든”이란 말이 들어가면, 지금 쓰이는 개념이 그 타입에 무관하다란 말과 같습니다. 한 가지 설명만으로 모든 경우와 맞서려 하면 머리가 복잡합니다. 그 때 그 때 어울리는 설명들을 가지고 헤쳐 나가야 합니다. 지금은 리스트를 값을 담고 있는 구조로만 해석하겠습니다. 이 구조가 모노이드 성격을 띄게 하면 내용물이야 뭐가 됐든 모노이드와 같은 동작을 하게 할 수 있습니다.

    instance Monoid [a] where
    mempty = []
    mappend xs ys = xs ++ ys

    ※ 리스트를 모노이드로 만들어 두었습니다. 이런 설명이 꼭 마음에 들진 않습니다. 이건 안에 들어 있는 내용물이 모노이드인게 아니라, 싸고 있는 구조가 모노이드인거란 생각이 듭니다. 공을 위로 쌓아 올리려면 동그란 구형이라 쌓기 어려우니, 네모 박스에 넣어서 쌓게 되면 이 공이 “쌓기 가능”한 특징이 생겼다라고 말하고 있습니다. 결론적으로 쌓는다는 목표에 도달했으니 공이 모노이드라 말하면 되는 걸까요? 한 가지 조건을 더 추가하자면 그냥 공과 박스에 든 공이 1대1 매핑되는 관계, 즉 isomorphic 하다면 공이 모노이드라 말해도 되지 않을까요?

    찝찝함은 남지만, 어쨌든 타입만 넘겨주면 모노이드로 만들 준비가 되어 있습니다. 이럴 때 Free란 말을 붙입니다. 리스트는 Free 모노이드를 만드는 도구입니다. Free는 공짜로라는 부사가 아니라, “Free 모노이드”가 고유 명사입니다. Free 모나드는 공짜로 모나드로 만들어 준다고 아니라, 그 자체로 하나의 모나드 종류입니다. IO 모나드, Reader 모나드, …Free 모나드입니다. Free 모나드가 Reader 모나드를 자동으로 만들어 주거나 하지 않습니다. 적절한 인터프리터를 만들어 Reader로 동작하게 할 수는 있습니다.

    Free 모나드는 이펙트를 합치는 작업을 하지 않는 모나드입니다.

    2022-7-27 추가 - 공을 연결하는게 아니라, 연결된 상자들을 준비하고, 상자에 공을 넣으면 “Free하게 공을 연결했다”고 합니다.↩︎

  3. 타입 생성자와 값 생성자 혼동

    이젠 안 할 때도 됐는데, 지금도 이런 실수를 자주 합니다.

    Free x = Free ( MyReader (\r -> (>>= f) (runMyReader mr r)) ) ---- (x)

    Free x의 모양이 Free (MyReader e a) 모양일 거라 오해할 수 있습니다. Free (MyReader e a)는 값이 아니라 타입입니다. 값은 Free 정의에 따라 Free (Free ...(Pure r)) 모양이지, Free (MyReader e a) 가 아닙니다.

    Free가 인자를 두 개 받아야 할 것처럼 오해 할 수 있습니다.

    * Control.Monad.Free> :t Free (Just (Free (Just 1)))
Free (Just (Free (Just 1))) :: Num (Free Maybe a) => Free Maybe a

    마지막 Just 1 을 괄호로 묶지 않아도 될 것처럼 보입니다. 여전히 타입 생성자와 값 생성자를 오해하고 있습니다. Free (Just 1) 은 Free Maybe a 타입입니다. Free 선언을 보면 값의 모양은 아래와 같습니다. (1을 위한 타입 제약 표시는 단순하게 보기 위해 뺐습니다.)

    data Free f r = Free 인자 하나 | Pure 인자 하나

    Free의 타입을 보면 복잡하게 나오지만, 결국 인자 하나를 받아 Free 타입이 되는 값 생성자입니다. 인자는 하나를 받지만, 타입 매개 변수는 두 개여서 살짝 혼동을 줍니다.

    *Main Control.Monad.Free> :t Free
Free :: f (Free f a) -> Free f a
       ^^^^^^^^^^^^^
         인자 하나

    저는 타입이 헛갈릴 때 Maybe를 넣어보곤 합니다. Maybe를 Free로 감싼다면

    Free Maybe r = Free (Maybe (Free (Maybe (Pure () )))) -- (X)

    일까요? 아닙니다. 값 생성할 때

    *Main Control.Monad.Free> :t Free (Maybe (Free (Maybe Pure () )))
<interactive>:1:7: error:
    • Data constructor not in scope: -- 값 생성자를 찾고 있습니다.
        Maybe :: Free f1 a1 -> f (Free f a)

    값을 구성하는 요소들 중 어디에 타입을 써주고, 어디에 값을 써주는지 알아야 합니다.

    *Main Control.Monad.Free> :t Free (Just (Free (Just (Pure ()) )))
Free (Just (Free (Just (Pure ()) ))) :: Free Maybe ()
    ↩︎
Github 계정이 없는 분은 메일로 보내주세요. lionhairdino at gmail.com