MonadFix

하스켈 위키 - MonadFix
MonadFix is Time Travel - Will Fancher
A Recursive do for Haskell

“자기가 반환하는 값을 인자로 받아서 실행”

생각 스트레칭
“미래값을 바꾸는 미래값을 요구하는 역설paradox”
무한이라든지, 아직은 없는 미래값이라든지 하는 말들을 보면, 머릿속에서 시뮬레이션하기 까다로워서 불편합니다. 불편한 이유는 우리가 너무 부지런해서 입니다. 값이 아직 다 필요하지도 않은데, 무한히 준비할 생각부터 하고, 미래값이 아직 필요하지도 않은데, 무슨 값일지 걱정해서 그렇습니다. 사실 이들 개념들은 적절히 파트너로 동작하는 함수들이 있거나, 아니면 알고 보니 알 필요 없는 값이다라는 식으로 동작합니다. 무한 리스트값들은 take 같은 함수들이 파트너로 반드시 있어야 실용적인 의미가 생기는 것처럼 말입니다. f undefined를 적절한 파트너와 함께 써서 오류없이 결과값을 얻을 수 있다면(해당 인자를 평가하는 순간 undefined 오류가 나는데, 특정 조건하에선 평가할 일이 없다면), fix에 넣어 줄 수 있습니다.

현실적으로 내가 아직 만들지도 않은 결과를 내가 참조할 수는 없습니다. 그런 일은 일어나지 않습니다. 패러독스 해결은 제3자가 개입하거나, 단계를 나누는 방법이 있을 수 있습니다.

시간이 개입하면 어찌되나 보겠습니다. 모두 동작은 같은 f지만, 다른 시점에 동작한 f는 다르다는 뜻으로 번호를 붙여 보겠습니다. - @todo 편하게 생각할 방법을 고민 중입니다.
fix f = f1 (f2 (f3 ...
f1은 f2의 결과를 받아 계산합니다. ※ f2가 f1과 다른 것이라 생각하면 좀 낫지 않나요?
하나 주의해서 볼 게, f1 (f2 (f3 (...)))는 함수 상태가 아닙니다. 어찌 됐든, 무한이긴 하지만, 미래의 값이긴 하지만, 인자를 준 상태입니다.

[1..] = fix (\xs -> 1 : fmap (+1) xs)  

xs는 다른 시간(미래)의 f의 결과값입니다. 어떤 값을 가질지는, 늘 그렇듯 Lazy하게 필요할 때 보면 됩니다. 처음 결과는 1 : ...값입니다. 아는데 까지만 써주고, 모르는 건 모르는 채로 두면 됩니다. 1만 필요하다면 여기서 끝이지만, ... 부분을 알고 싶다면, 또 다른 f를 실행하면 됩니다. 이제 ...을 알기 위한 현재 f는 미래 f의 결과값 1 : ... 값을 가지고 실행하면 적어도 1 : (1 + 1) : ...까지는 알 수 있는 상태가 됩니다. 반복하면, (fmap (+1)을 적용한 걸 +1로 표기) 1 : 1+1 : 1+1+1 : 1+1+1+1 : ...이 나옵니다. 파트너 take와 같이 쓰면,

ghci> take 5 $ fix (\xs -> 1: fmap (+1) xs)
[1,2,3,4,5]

전혀 알 수 없는 미래값에 대해선 위와 같이 할 수 없습니다. 미래값에 의존해서 실행한 함수 결과에는 적어도 1:이 들어가 있는 걸 알기 때문에 벌어지는 일입니다. 미래값이 뭔지 모르는데, 현재에서 미래값을 참조하는 일이 어떻게 의미를 가질까의 비밀은 여기 있는 건지도 모르겠습니다. 어떤 미래값으로 돌리든 예정되어 있는 일부 결과 모양을 알아야만 cyclic 정의가 의미가 있습니다.

또 다른 예시로, 피보나치 수를 fix로 구하는 걸 보겠습니다.

fix (\fib -> 0 : 1 : zipWith (+) fib (tail fib))

매직이 일어나는 것처럼 보이지만, 사실은 미래 결과를 받아서 돌린다 한들 알 수 있는 건 0과 1만 있을 뿐입니다.

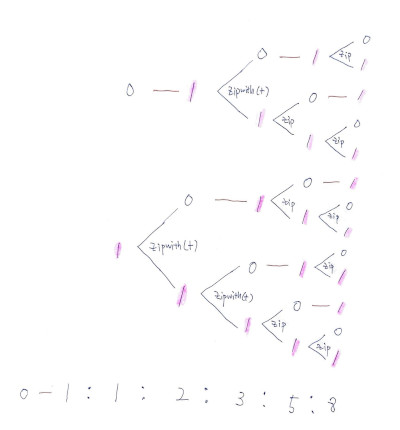
0:1:<thunk> ----------- f -----------> 0:1:<thunk>

f가 인자로 자신의 결과값을 받아서, 한 번 실행하면 0:1:<thunk>결과를 얻습니다. 미래의 자신이 돌리든, 과거의 자신이 돌리든, 결과에 0:1이 있는 것만은 알고 있다는 뜻입니다. f가 받는 인자도 0:1:<thunk>고, 결과값도 0:1:<thunk>입니다. f a = a로 말하면 f에 입력으로 준 것도 a이고, 결과도 a입니다. 이 때 a를 고정점이라 부릅니다. fix f로 0:1:<thunk>를 얻었는데, 이 걸 f의 입력값으로 f (fix f) - f(0:1:<thunk>) 다시 넣어줘도 인자와 결과값 둘이 같다는 뜻입니다. f 함수의 고정점은 fix f입니다.

<thunk>를 평가할 일이 생기면, 또 다시 f를 실행해서 얻은 결과를 zipWith (+) [0,1,<thunk>] [1,<thunk>] 하는 절차가 한 번씩 돌고 있습니다.

f(f(f(...))) = (f(f(...))) 이란 뜻입니다. f를 적용하나 안하나 같은 값을 찾는다면, 명쾌하기도 하고, 허탈하기도 한 f가 무한히 적용되어 있는 값을 고르면 된다는 뜻입니다. 단, fix f가 유일한 고정점이라 말하는 건 아닙니다.

여기까지가 fix의 동작 요약입니다. 이제 mfix로 넘어가 보겠습니다.

mfix

값 재귀를 위해 mfix 메소드를 정의합니다. 직접 mfix를 쓰는 경우도 있고, RecursiveDo 확장을 통해 사용되기도 합니다.

class Monad m => MonadFix m where
  mfix :: (a -> m a) -> m a

먼저 타입으로만 추측하여 읽어 보면,

fix  :: (a ->   a) ->   a
mfix :: (a -> m a) -> m a

MonadFix is just a monadic version of fix

fix f의 결과는 f(f(f(f... 이런 모양이 되니, mfix f도 아마 f(f(f(f... 이런 모양일텐데, 한 겹 넘어갈 때마다 effect m을 어찌하고 있는지만 찾으면 될 것만 같습니다. (뒤에 잘못된 접근인 걸 보입니다.) fix는 일반 함수지만, mfix는 MonadFix클래스의 메소드로 타입마다 다른 인스턴스를 가지고 있습니다. 그런데, 특정 모나드에서는 아래 코드로 해결할 수도 있습니다.

mfix f = fix (>>= f)

단, fix함수는 인자가 strict인 함수를 받지 못하기 때문에, (>>=)가 strict한 인스턴스에선, 이 mfix를 쓸 수 없습니다. fix함수는 (a -> a) -> a타입이니, (>>=):m a -> (a -> m b) -> m b에 두번 째 인자로 f:a -> m a를 줘서 (>>= f):m a -> m a로 만드니, fix에 넣어 줄 수 있습니다.

Maybe의 경우 아래같이 돌리면 무한으로 가버립니다.
(무한으로 가지 않는 mfix 인스턴스가 이미 정의되어 있어, 여기서는 mfix'으로 이름지었습니다. )

mfix' f = fix (>>= f)

ghci> mfix' $ \_ > Just 1 -- 원래 mfix는 Just 1이 나온다.
<무한 실행>

mfix는 (((...) >>= f) >>= f) >>= f 이런 모양이 나옵니다. 차근 차근 쫓아가 보겠습니다.

mfix' (\_->Just 1) = fix (>>= (\_->Just 1))
                   = (>>= (\_->Just 1)) (fix (>>= (\_->Just 1))) -- 편의상 표기
                   = (fix (>>= (\_->Just 1))) >>= (\_->Just 1)
                   = ((...) >>= (\_->Just 1)) >>= (\_->Just 1)

눈에는 (\_->Just 1)이란 게 보이니, 뭐가 됐든 Just 1이 나올테니, Lazy하게 볼 수 있다면 굳이 미래를 모두 평가할 필요가 없는 게 보입니다. Fancher의 글에선 (...)부분을 미래라 말하고 있습니다. 가장 먼 미래에서 시작해서 무한히 >>= (\_->Just 1)을 반복하는 것으로 해석할 수 있습니다. mfix'은 ...부분에 Nothing이 있는지 계속 찾아야만 합니다. 그래서 무한 실행에 빠지고, 마찬가지로 IO도 무한 실행하지만 스택이 꽉 차버립니다.

ghci> mfix' (\_ -> print 1)
*** Exception: stack overflow

인스턴스 정의 목록을 보면, IO, Maybe, [], ST, Either 등 많은 수가 별도의 인스턴스를 정의하고 있습니다. 바인드들에게 undefined를 주며 테스트 해 볼 수 있는데, 조금 사례를 찾아보니 Reader 모나드 바인드 정도는 mfix'으로 가능했습니다. 결론에서 추가로 설명하겠습니다.

ghci> flip runReader 0 $ undefined >>= \_ -> reader (\_ -> 1)
1
ghci> flip runReader () $ mfix' $ \_ -> reader(\_ -> 1)
1
ghci> runWriter $ undefined >>= \_ -> writer (2,"b")
(2,"*** Exception: Prelude.undefined

처음엔, fix와 유사한 동작을 할 것이다란 생각으로 위와 같이 접근했는데, mfix의 목적이 a -> m a의 고정점을 찾는 게 아닙니다.

왜 필요하지?

mfix는 fix의 모나딕 버전이니, 이펙트가 있는 작업 즉, 액션을 반복시킬 때 쓰겠거니 생각할 수 있는데, 액션 반복은 fix로도 됩니다. 아래 코드는 Roman Cheplyaka - MonadFix example에서 발췌했습니다.
※ fix f에서 f가 받는 함수가 m a -> m a일 뿐(a -> a에서 a자리에 m a)입니다. 아래 \repeat가 받는 값은 m a입니다.

guessNumber m = fix $ \repeat -> do -- 액션도 fix로 반복할 수 있습니다.
  putStrLn "Enter a guess"
  n <- readMaybe <$> getLine
  if n == Just m
    then putStrLn "You guessed it!"
    else do
      putStrLn "You guessed wrong; try again"
      repeat

\repeat이 받는 함수가 a -> m b로 오해할 수 있는데, 아래와 같은 상황입니다.

ghci> let f = \repeat -> do repeat 
ghci> f $ print 1 -- IO ()를 받고 있다.
1
ghci> :t f
f :: p -> p

fix만으로 무리 없이 돌아갑니다. 그럼 아래같이 피보나치수를 구하는 경우는 어떨까요?
※ 비교 fib = 0 : 1 : zipWith (+) fib (tail fib)

fibIO1 = do
  putStrLn "Enter the start number"
  start <- read <$> getLine
  return $ start : 1 : zipWith (+) fibIO1 (tail fibIO1)

타입 체커를 통과하지 못합니다. fibIO1은 리스트가 아니라, 리스트를 만들어 내는 액션입니다.

이제 mfix :: MonadFix m => (a -> m a) -> m a를 써보겠습니다.

fibIO3 = mfix $ \fib -> do
  putStrLn "Enter the start number"
  start <- read <$> getLine
  return $ start : 1 : zipWith (+) fib (tail fib)

위에 fix 예시에서 그랬던 것처럼 fix (>>=f)에서 (>>=f)는 계속 실행되어, 실행될 때마다 "Enter the start number"...getLine이 돌아 계속 입력을 받게 될까요?

※ 순환cyclic정의를 할 때 Tying the Knot이란 동작이 있습니다. Lazy하게 동작하니, 필요한 곳까지만 가면 됩니다. 이 필요한 곳을 매듭knot이라 부릅니다.

위 fibIO 예시 자체가 살짝 억지스럽긴 합니다만, 동작을 보는데 문제는 없습니다. 원하는 동작은 이펙트를 만들어내는 액션 동작은 딱 한 번만 실행되고(effectful하게 외부에서 start값을 입력받습니다.), 그 후에는 액션이 아닌 값만 가지고 반복해야 합니다. 마치 \fib -> ... 에서 ... 부분이 통채로 반복될 것만 같은 겉모양인데, \fib에는 미래 함수의 결과값 start : 1 : zipWith (+) fib (tail fib)가 들어가긴 할텐데, 그 미래 함수가 실행될 때 getLine이 또 실행되어야 하는 것 아닐까 혼란스럽습니다. 그렇게 동작하는 건 바로 fix함수가 m a -> m a를 받았을 때의 동작입니다.

mfix는 a -> m a를 위해서 만들었습니다. 그런데, fix가 a -> a를 받아 고정점을 찾듯, a -> m a의 고정점을 찾는게 아니라, 인포멀하게 얘기하면 m을 한 번만 동작하게 하고, m을 제외한 a -> a의 고정점을 찾는 게 목적입니다.

위 fibIO3에서 보면, mfix가 (a -> m a)를 받아야 하니 \fib로 들어 오는 건 m a가 아니라 a입니다. "Enter the start number" 같은 이펙트풀한 동작이 없을 거라 예상할 수 있습니다. 실제 동작을 보기 위해, 실제 라이브러러리에 있는 IO 인스턴스 구현을 보겠습니다.

-- Control.Monad.Fix
instance MonadFix IO where
    mfix = fixIO

fixIO :: (a -> IO a) -> IO a
fixIO k = do
    m <- newEmptyMVar -- mutable 변수를 만들고,
    ans <- unsafeDupableInterleaveIO -- 미래 값을 예측하고
             (readMVar m `catch` \BlockedIndefinitelyOnMVar -> -- 블록 에러 패턴매칭
                                    throwIO FixIOException)
    result <- k ans -- 미래값 ans에 k를 적용한 후, result에 effect없는 값을 넣고 있다.
                    -- 이 값은 완성된 결과값이 아니라, 일부만 알고 있는 결과로,
    putMVar m result -- 미완성 값을 넣어 놓는다. MVar 안에는 액션이 아닌 값result이 들어 있다. 
    return result

unsafeDupableInterleaveIO :: IO a -> IO a
IO 컴퓨테이션을 Lazy하게 할 수 있습니다. IO a 타입을 받고, a를 요구demand하는 곳이 있을 때 계산을 합니다. readMVar의 반환값은 IO a로 이 a가 필요한 순간이 되어야만 readMVar를 실행합니다. ans는 thunk를 받은 상태입니다.

어디선가 ans가 평가될 때 readMVar가 실행될 겁니다.

fibIO3은 return (start : 1 : zipWith (+) fib (tail fib))를 반환합니다. 어디선가 zipWith~ 부분에 대한 요구demand가 생겨 평가하게 되면, fib는 MVar에 저장해 두었던 미래 함수의 결과ans를 가져 옵니다. 그 미래 함수의 결과는 또 더 미래 함수의 결과를 참조하고 있습니다. (하지만, 미래의 완전히 알 수 없는 어떤 값이 아니라, 미래에 생길 값에 대해 일부는 알고 있습니다.)

k에 \fib -> do ... return $ ... zipWith (+) fib (tail fib)를 넣어주면, \fib에는 나중에 결정될 미래값 ans가 들어갑니다. 이 후 일들은 return 안 쪽에서 일어나는 일들입니다. (start로 0을 넣었다 치면) return $ 0:1:<thunk>을 했습니다. 어디선가 패턴매칭이 일어나서 <thunk>를 평가하려 들면, zipWith (+) [0,1,<thunk>] [1,<thunk>]을 평가합니다. 그럼 다음 원소 1을 돌려 주고, 또 <thunk>로 다음을 대기합니다. 더 달라고 하면 또 [0,1,<thunk>]에 있는 <thunk>와 [1,<thunk>]에 있는 <thunk>를 평가하게 될 겁니다. 위에 피보나치 그림 참고. MVar는 순서대로 평가되는 IO에서 아직 없는 값을 표현하기 위한 수단입니다.

아직은 간단히 설명을 못하고 있는데, 아래 예시와 같은 상황입니다. repeat는 이펙트 없이 무한 반복할 거라 해놨습니다. 하지만, 미리 동작하진 않고 나중에 take가 달라면, 달라는 만큼만 동작하고, 여전히 무한히 동작할 상태(<thunk>)에 머무릅니다.

ghci> result <- return $ repeat 1
ghci> take 10 result 
[1,1,1,1,1,1,1,1,1,1]

인포멀하게 얘기하면, fixIO 전체가 아니라, 오직 k ans 부분만 반복한다는 말입니다.

mdo

Imperative cyclic linked lists 하스켈 위키에 있는 예시를 보겠습니다.

data Node = Node Int (IORef Node)
mknode = mfix (\p -> do
    p' <- newIORef (Node 0 p)
    putStrLn "node created"
    return p')

첫 번째 노드까지만 알면 되면 (Node 0 <thunk>)에서 평가를 멈출테고,
다음을 요구한다면, 안에 있는 <thunk>를 평가해서 (Node 0 (Node 0 <thunk))이 됩니다. 마치 이미 만들어진 값이 아니라, 제너레이터를 품고 있는 느낌입니다.

main = do
  p <- mknode
  Node x q <- readIORef p -- Node 0 <thunk>
  print x -- 0 출력
  Node y _ <- readIORef q -- 위 <thunk>를 평가한 결과는 Node 0 <thunk>
  print y -- 0 출력

이제 다음 예시가 실용에서 많이 만날 동작입니다.

mk2nodes = mfix (\ ~(p,r) -> do
    p' <- newIORef (Node 0 r)
    r' <- newIORef (Node 1 p')
    putStrLn "nodes created"
    return (p',r'))
  >>= \(p,r) -> return p
-- 보기 좋게 한 줄로 축약해서 보면 mfix (...) >>= \(p,r) -> return p 모양입니다.

※ 인자에 붙은 틸드~는 Lazy하게 평가하겠다는 뜻입니다.
미래값 r을 다음으로 하는 노드 p'을 만들고,
p'을 다음으로 하는 노드 r'을 만들고,
미래값 p에는 p'을, r에는 r'을 넣어 줍니다.

cyclic이 잘 보이게 미래값을 받은 상태로 읽는다면,
r을 다음으로 하는 p를 만들고
p를 다음으로 하는 r을 만들었습니다.

순환cyclic 정의를 하고 있습니다.

main = do
  p <- mk2nodes
  Node x q <- readIORef p
  print x
  Node y r <- readIORef q
  print y
  Node z _ <- readIORef r
  print z

앞으로 mfix를 쓰려면 습관적으로 미래값에 대응될 값들을 p', r' 식으로 쓰면 좋을 것 처럼 보입니다.
바로 이를 위한 Syntactic sugar mdo가 있습니다. do를 쓸 자리에 mdo를 쓰면 mfix를 돌려 cyclic 정의를 하겠다는 뜻입니다.

mknode = mdo
  p <- newIORef (Node 0 p)
  putStrLn "node created"
  return p

mk2nodes = mdo
  p <- newIORef (Node 0 r)
  r <- newIORef (Node 1 p)
  putStrLn "nodes created"
  return p

이제 정의 순서와 상관없이 do 안에서 바인딩을 cyclic하게 쓸 수 있게 됐습니다.

do 안에서도 순환 정의를 하겠다고, 이렇게 독하게 체계를 만들어 낸 사람들이 존경스럽습니다.

결론

“mfix는 액션 전체가 아니라, 결과값만 재귀시켜도 될 때만 의미가 있습니다.”
“mfix는 액션 전체가 아니라, 컨텍스트 안에 있는 결과값만 재귀시키기 위해 만들었습니다.”

mfix로 a -> m a함수를 감싸면, m은 한 번만 영향을 미치고, m이 없는 a -> a를 재귀 돌려 m (재귀 결과)값을 반환합니다.

처음 개념을 봤을 때는,

※ 잘못된 접근 - 아래는 틀린 내용입니다.
애초에 액션 a -> m a는 고정점이 있을 수가 없습니다. a를 입력 받고, 출력으로 m a를 내뱉으니 있을 수가 없습니다. 그런데 모나드에서 처럼 m a -> m (m a)로 보고, join이 존재한다면 고정점(고정점이라 우길 수 있는 것)을 찾을 수 있을 겁니다. (모나드에서 a -> m b 액션에 m a를 넣어줘서 m (m b)가 나오면 join을 해서 m으로 맞춰 줬습니다.) join을 μ로 표기하면

f(μf(μf(...))) = f(μf(μf(μf(...))))

이런식으로 반복하게 될겁니다. 근데 이 때 μ가 계속 스택을 잡아 먹거나, 혹은 계속 인과관계가 있다면, 정보를 무한히 갖고 있어야 하니 의미 있는 일을 할 수 없을 겁니다. μ가 trivial한 일을 하는 거라 (Reader같은 것들) 마지막에 한 번만 해줘도 되는 것들이라면, 즉 m a -> m (m a) 에서 a -> a로만 무한 반복 시키고 m(return)을 나중에 한 번만 붙여도 의미가 달라지지 않는 것들만 mfix가 가능하다고 보고 있습니다.

라고 오해 했습니다.

이론상은 fix (>>= f)가 mfix 구현이고, 이 걸로 그냥 돌리면 무한히 실행되어 의미가 없을 때, 무한히 돌지 않아도 의미 있는 결과를 내는 mfix를 별도로 만든 게 아니라, mfix는 컨텍스트 안에 있는 값을 재귀 시키기 위한 것입니다.

“Value Recursion in Monadic Computations”

이펙트가 여러번 발현되든, 한 번 발현되든 의미가 다르지 않은 일부 모나드에선 이 동작을 fix (>>= f)로 써도 같은 동작을 한다는 뜻이지, 모든 모나드의 mfix가 fix (>>= f)와 같은 동작을 한다는 얘기가 아닙니다. (검증 필요)

MonadFix의 아래 성질이 오해한 부분을 명확히 보여 주는 것 같습니다.
purity 법칙: mfix (return . h) = return (fix h)

일부 문서에서 fix (>>= f)를 먼저 보여주며, MonadFix is just a monadic version of fix라 해서, 오히려 혼란스럽게 접근한 건 아닌가 합니다.

※ Maybe 인스턴스의 경우, Nothing인지 계속 살펴봐야 하지만, 무조건 Just라 놓고 실행하다 Nothing을 만나면 폭파!시켜버리는 편법?을 쓰고 있습니다.

-- Control.Monad.Fix
instance MonadFix Maybe where
    mfix f = let a = f (unJust a) in a
             where unJust (Just x) = x
                   unJust Nothing  = errorWithoutStackTrace "mfix Maybe: Nothing"

무한한 미래를 참고하는데, “미래에도 절대 Nothing”이 없어야 Just라고 해야 할 것 같은데, 당장 필요한 것만 봐서 Just라고 하니, 이래도 되나 싶은 생각이 들긴 합니다만, 어쨌든 저렇게 구현되어 있습니다.

무한에 재귀에 이펙트에… 머리를 복잡하게 하는 것들이 다 섞여 있는 주제인데, 이 게 읽기 편해지면 하스켈로 프로그래밍하는데 조금이라도 도움이 되긴 하겠지요?

생각 스트레칭

(.) f g   = \x -> f (g x)

(.)은 모나드 (>=>)의 특별 버전으로 볼 수 있습니다.

(>=>) f g = \x -> f x >>= g