여기 글들은 일종의 질문입니다. 용어 선택도 학계, 업계에서 쓰는 걸로 되어 있지 않고, 틀린 내용이 있을 수도 있습니다.
카테시안 카테고리, 프로덕트 카테고리, 2카테고리, 바이카테고리를 거쳐 모노이달 카테고리에 도착했는데, 다른 텍스트에선 명시적으로 언급하지 않는, 실용적인 상상이 떠올라 글을 남깁니다. 카테고리 이론을 정교하게 설명하기에는 지식이 부족하니, 엉성한 글을 읽지 않으시려면 바로 정리 섹션으로 건너뛰셔도 좋습니다.
아래는 전공자 혹은, 유관 전공자 분들이 보시고 이상한 생각이라 했던 내용들이 다수 들어가 있습니다. 조심해서 신뢰 없는 브레인 스토밍쯤으로 의심하며 보세요.
어떤 결과에 도달하기 위해서 해야 되는 절차가 1단계가 있는 걸, 절차를 2단계를 거치게 하면 어떤 효과, 장점이 있을까요?
1단계 밥을 먹는다.
1단계 씻고
2단계 밥을 먹는다.
1단계 - 1.1 얼굴을 씻고
- 1.2 손을 씻고
2단계 밥을 먹는다.“2단계로 되어있는 시스템”은 “1단계로만 이루어진 시스템”을 표현 할 수 있습니다. 결과에 영향을 미치지 않는 “아무 것도 안함”이란 동작을 만들어 두면
1단계 아무것도 안함
2단계 밥을 먹는다.이 걸로 “1단계만 있는 시스템”을 표현할 수 있습니다.
총 3단계처럼 보이는 세 번째 예시의 경우는 각 단계마다 받을 수 있는 절차가 더 세분화되어 여러 절차가 하나의 큰 절차로 표현할 수 있습니다. 아래로 갈수록 더 많은 케이스를 표현할 수 있는 표현력이 생기는 걸 알 수 있습니다. 절차를 나누는 것과, 아무것도 안함을 이용해 좀 더 일반화 됐다고 볼 수 있습니다.
※ 저는 이 3단계가 모노이달 카테고리의 모노이드와 비슷하게 보입니다. 이 말에는 많은 상상이 들어가 있습니다.
어떤 시스템에 이항 연산이 있고, 항등원이 존재하고, 이 이항 연산이 결합 법칙을 만족하고 닫혀 있으면 어떤 것이든 모노이드라 부릅니다.
결합 법칙과 이항연산이 있는 반군semigroup은 집합에서 두 원소를 꺼내 이항연산을 적용하면, 다시 집합내의 한 원소가 나옵니다. 여기에 항등원 조건을 넣으면 어떤 변화가 생길까요?
자연수와 이항 연산으로 더하기의 동작을 보면
1 + 1 = 2
1 + 2 = 3
...
100+1000 = 1100
...자연수의 모든 수를 더하기를 이용해 표현할 수 있습니다. 보통은 자연수 둘을 연산해서 자연수가 나오는, 최종 자연수라는 것으로 설명하는데, 여기서는 다음과 같이 항등원의 필요성이 잘 보이게 조금 비틀어서 상상해 봤습니다. (같이 공부를 하며, 여러가지 알려주던 분들이 너무 자기 생각에 빠졌다 했던 생각인 만큼, 믿고 보진 마세요. 이런 아이디어도 있구나란 생각으로 보시기 바랍니다.)
어차피 모든 _ + _는 이항 연산을 통해 하나의 자연수가 됩니다. 이 걸 최종 모양으로 가기전 +가 들어가 있는 모양으로 모두 표현하는 걸로 바꿔서 바라 봤습니다.
2는 1 + 1로 표현할 수 있고,
3은 1 + 2로 표현할 수 있는데,
1은 어떻게 할까요?+ 이항연산과 만나면 아무일도 하지 않는, 즉 +연산의 항등원 0을 시스템에 추가하면 0포함 모든 자연수를 한 가지 모양 _ + _으로 표현할 수 있게 됩니다. 보통 연산이 작업을 끝내서(모두 reduce해서), 자연수에 도달한 모양으로 보는데, 항등원의 동작을 보기 위해 연산을 넣은 상태를 봤습니다.
0은 0 + 0
1은 1 + 0
2는 1 + 1
...항등원이 추가 되면, 비로소 모든 원소를 한 가지 모양으로 표현할 수 있습니다. 다시 말하지만, 보통의 텍스트에선 위 연산을 reduce해서 자연수로 같아짐을 보입니다. 여기서는 0이 잘보이게 위 상태로 멈춰 놓았습니다. (타입에는 함수를 넣어 놓을 수 있습니다. 저는 여기서 +가 타입으로 보이기도 하는데, 이와 관련된 얘기는 별도로 올리겠습니다.)
집합에서 원소들이 모노이드가 되는 동작을 보듯, 카테고리에서도 한 카테고리에서 두 개의 대상object을 뽑아, 어떤 연산을 거치면 다시 같은 카테고리의 원소가 나와야 합니다. 카테고리간 연산은 펑터로 표현됩니다. 카테고리 하나와 하나를 매핑하는 건 펑터였고, 카테고리 둘에서 하나로 매핑하는 건 바이펑터(이항펑터bifunctor)라 부릅니다. 모노이드와 마찬가지로 바이펑터가 결합 법칙을 따르고, 항등 법칙을 따라야 모노이드 성질을 같게 됩니다. 추상 대수에서 처럼, 아무런 별도 처리 없이 결합 법칙을 따르고, 항등 법칙을 따르는 게 아니라, 다음과 같이 조건을 위한 새로운 절차를 추가합니다.
A ⨂ (B ⨂ C) = (A ⨂ B) ⨂ C 그냥 이렇게 결합 법칙을 만족하는 게 아니라,
α_{ABC}: A ⨂ (B ⨂ C) -> (A ⨂ B) ⨂ C※ 코드 모양에 아래 첨자 표기가 안되어, {A}모양으로 표기했습니다.
그냥은 같지 않을 수도 있지만, α라는 절차를 거치면 같아집니다.
항등 법칙도 마찬가지입니다.
그냥은 안될 수도 있지만, 좌 항등원은 λ라는 절차가 있고, 우 항등원은 ρ라는 절차가 있으면 항등원이 됩니다.
λ_{A}: I ⨂ A -> A
ρ_{A}: A ⨂ I -> A왜 모노이달 카테고리에선 α, λ, p를 두었을까요? 생각 스트레칭에 쓴 것과 같이 좀 일반화하기 위한 장치가 아닐까요?
αABC에는 아래 첨자 {ABC}가 있고, λA, ρA에는 아래 첨자 {A}가 있습니다. 이 말은 모든 세가지 구성원 조합마다 α가 각 각 있고, 모든 구성원 각각 별 개로 λ, ρ를 가지고 있다는 얘기입니다. 이러면 결합 법칙, 항등 법칙이 성립하지 않는 경우가 있을까 싶은 막무가내 규칙처럼 보이기도 하는데, 깊이 들어 가보질 못해, 이런 조건이 어떤 결과를 가져오는지 궁금합니다. 특별히 이들 α, λ, p가 모두 identity이어서 아무 일도 하지 않는 경우를 strict monoidal category라 합니다. (하스켈에서 모나드를 얘기할 때 만나는 엔도펑터 모노이달 카테고리는 strict monoidal category입니다.)
엔도펑터 T를 대상으로 가지고 있는 카테고리를, 바이펑터 ⨂로 펑터 합성⋅을 넣어 모노이달 카테고리를 만들고, 펑터 합성⋅으로 만들어진 T ⋅ T를 하나 뽑고, 여기에 T ⋅ T -> T 가 있으면 모나드라 합니다. 매우 불친절한 설명입니다.
지금부터 제가 이해한 방법으로 설명을 하는데, 상상이 많이 들어가 있습니다.
모노이드의 이항 연산을 아래와 같이 절차를 쪼갭니다.
위의 생각 스트레칭에서 얘기했던 아이디어를 한 번 더 적용하겠습니다.
구성원 둘을 받아 하나로 만드는 작업은 “둘을 받아오는 작업”, 이렇게 받아 온 ““둘을 하나로 만드는 작업”” 둘로 나눠 볼 수 있습니다. 한 번이었던 절차가 두 번이 됐으니, 조금 더 일반화 됐다고 볼 수 있습니다.
이항 연산multiplier----> 2번: 하나로 만드는 작업join . 1번: 둘을 붙이는 작업(bifunctor)모노이드에서 얘기했던 것과 비슷하게, 카테고리가 모노이달 카테고리이면, 모든 구성원은 바이펑터가 적용된 모양으로 볼 수 있습니다. 즉 “1번 둘을 붙이는 작업”은 바이펑터로 넣은 펑터 합성으로 이미 모든 구성원이 갖고 있다고 볼 수 있습니다. 이제 둘을 “2번 하나로 만드는 작업”이 있으면 모노이드의 이항 연산이 될 수 있습니다.
보통 펑터 합성을 가운데 점cdot ⋅으로 표시합니다.
“펑터 합성”과 “함수 합성”의 차이
Maybe와Mabye를 함수 합성한다면, 마치 값 생성자Just를 두 번 써서Just(Just 1)로 표현하면 될 것처럼 보입니다. 하지만 펑터는 한 가지 작업만을 의미하는 게 아닙니다.Maybe의 경우는Just와Nothing이 있습니다. 처음 둘을 다음 둘과 합성하는 걸, 함수 합성으로는 표현할 수 없습니다.
Maybe와[]를 합성한다면 값 수준에서는 타입이 달라, 함수 합성처럼 생각하면 합성할 수 없습니다. 타입 수준 합성으로 생각하면Maybe [_]혹은[Maybe _]가 됩니다. 펑터 합성은 타입 수준 합성으로 생각해햐 합니다. -@다믜님이 타입 레벨 합성에 대해 알려주셨습니다. 감사합니다.
모노이드가 되려면 결합 법칙과 항등 법칙을 따라야 합니다.
“2번 둘을 하나로 만드는 작업”을 join이라 부르고, 법칙들을 따르는지 쫓아가 보겠습니다.
T ⨂ T ⨂ T가 있을 때
join(join (T ⨂ T) ⨂ T) = join(T ⨂ join(T ⨂ T))먼저 하나로 만들든, 나중에 하나로 만들든 결과가 같아야 합니다.
join : (T ⨂ T) -> Tjoin은 위와 같은 작업을 하는 매핑입니다.(여기서 세세한 구현까지 생각할 필요는 없습니다.)
join(join (T ⨂ T) ⨂ T) = join(T ⨂ join(T ⨂ T))
join( T ⨂ T) = join(T ⨂ T )
T = T다음은 항등 법칙을 보겠습니다.
join(T ⨂ I) = join(I ⨂ T)I는 ⨂의 항등원입니다.
위가 성립하게 만들어야 하는데, join은 T가 둘인 경우만 적용할 수 있습니다. join을 적용하기 전에 T를 추가해주는 작업이 필요합니다.
return: I -> Treturn이 있으면 아래같이 join 연산에 항등원 역할을 하도록 만들 수 있습니다.
join(T ⨂ return I) = join(return I ⨂ T)
join(T ⨂ T) = join(T ⨂ T)
T = T즉 이 시스템은 join이 이항 연산 역할을 하고, return이 항등원 역할을 하는 모노이드가 됩니다.
정리해서 말하면 1번 둘을 붙이는 작업⨂은 이미 되어 있는 시스템은 join, return이 있으면 모노이드가 됩니다.
⨂로 모노이달 카테고리일 때, 오브젝트 중 join, return 이 있는 것은 모노이드가 됩니다.
엔도펑터가 펑터 합성 ⋅으로 모노이달 카테고리일 때, 그 중 어떤 한 엔도펑터(ex. Maybe, [], Reader, Writer…)가 join, return이 있으면 모노이드가 됩니다.
※ 하스켈에서 펑터 합성은 보통 생략해서 Maybe ⋅ Maybe가 아닌 Maybe (Maybe a)로 보통 만납니다.
모나드는 엔도펑터 모노이달 카테고리의 대상object중 모노이드인 대상입니다.
“엔도펑터
T”를 오브젝트로 하는 카테고리C는[C(T), ⊗, id, α=id, λ=id, ρ=id]가 모노이달 카테고리일 때, 이 중 오브젝트 하나T를 뽑고,⊗으로functor composition을 주면,[T, μ, η ]가 모노이드가 될 때, 엔도펑터T를 모나드라 부릅니다.
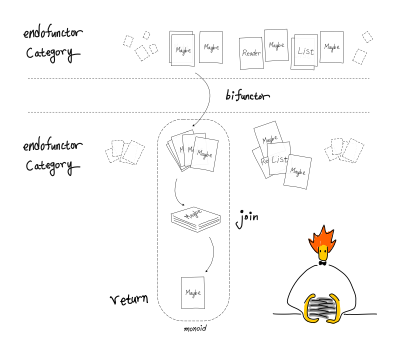
제가 보는 핵심 아이디어는 “이항 연산을 두 번의 절차로 나눠 놓은 것”입니다. 두 번의 절차 중 한 절차는 이미 디폴트처럼 가지고 있는 시스템에서 모노이드를 만들려면, 나머지 한 절차를 추가해서 보면 됩니다. 아래 정리에 도달하려고 지금까지 길게 설명을 적었습니다.
1 (=1+0), 2 (=1+1), 3 (=1+2) ...즉, 자연수를 타입으로 놓으면
타입 =타입같음= 타입 "연산" 타입으로 모두 같은 이항 연산 모양(같은 타입)으로 볼 수 있습니다.
하지만, 이펙트가 있는 경우는 이렇게 안됩니다.(Identity 경우는 되니 항상 안된다고 말할 순 없고, 거의 안된다고 말해야겠습니다.)
타입 =타입같음=? 타입 "이펙트가 있는 연산" 타입이럴 때 아래와 같이 절차를 한 번 더 두어 표현력을 늘릴 수 있습니다.
타입 =타입같음= join ( 타입 "이펙트가 있는 연산" 타입 )Maybe 엔도펑터를 예를 들면,
Maybe =타입같음= Maybe ⋅ Maybe가 아니지만
Maybe =타입같음= join (Maybe ⋅ Maybe)가 될 수 있습니다.더 정확히 말하면, join과 return을 잘 정의할 수 있다면 모노이드로 만들 수 있습니다.
더 공부하면, 또 깊은 뜻을 알게 될지도 모르지만, 지금은 “이항 연산의 일반화”가 가장 눈에 들어오는 특징입니다. (생각을 검증해 주신 @Ailrun님 감사합니다. - 혹 여기 글에 틀린 설명이 있을까봐 부연하자면, 여기 설명 자체를 읽고 검증해주신 건 아니고, 아이디어를 말씀 드렸을 때, 다른 데서 볼 수 없는 모노이달 카테고리에 대한 자세한 설명과, 생각이 맞는 길로 가고 있다 정도를 알려주셨습니다.)
세세한 조건은 잠시 빼두고 제가 생각하는 핵심만 뽑아보면
두 구성원(원소)을 받아 작업을 한 후 하나의 구성원이 된다에서, (모노이드)
두 번의 작업(펑터)이 한 번의 작업과 같아지는 걸로 개념이 확대된 모노이드 (모노이달C 모노이드)가 됐습니다.
1 + 2 = 3 (모노이드)
Mabye(Maybe a) -> Maybe a (모노이달C 모노이드)
마치, 결론은 값에서 Computation으로 확장한 것처럼 됐습니다.
둘 사이에 모노이달C를 끼워 넣자면, 다음처럼 상상할 수 있습니다.
모노이달C는 모노이드와는 다르게 (늘상 모든 바이펑터가 그런지는 아직 잘 모르겠습니다.)두 번의 작업을 받아 붙여?놓되, 각 작업에 개별 접근이 가능한 상태입니다.
(ex, 2튜플 (x, y)은 “하나”가 됐긴한데, x, y를 구분해서 접근이 가능한 상태입니다. - 텍스트들에서 따로 구별해서 지칭하지 않아 적당한 용어를 모르겠습니다.) 둘을 붙이는 것과, 둘을 하나로 만드는 걸 보다보니, 둘이 하나가 된다는 건, 정보를 일부 잃어버리면서 돌아올 수 없는 길을 가는 것으로 보입니다. 붙이는 것보다는 더 인위적인, 덜 자연스러운 동작으로 보입니다.
모노이드
모노이달 카테고리
모노이달 카테고리에 있는 모노이드
차이를 정리 하면,
값 같은 경우는 Computation 절차가 사라지며, 하나가 되는데 (모노이드)
Computation을 합치면 Computation · Computation 처럼 히스토리?가 보이는 상태로 합칩니다. (모노이달C)
Computation · Computation을 모노이드처럼 히스토리를 날리며 하나로 만듭니다. (모노이달C 모노이드)
이항 연산의 일반화로 모노이드의 일반화 즉, 좀 더 모노이드의 본질을 생각하는데 개인적으론 도움이 됐는데, 맞게 생각하는지 확신은 없습니다.
(아마도, 이 말은 더 더욱 욕을 먹을 수도 있는데, 이렇게 생각을 확장하는데 아이디어가 되는 바탕은 모든 값을 Computation으로 보는데서 시작하지 않았을까란 생각입니다. 이 건 다른 글에서 더 떠들어 보겠습니다.)
Q. 이항binary이어야지 결합 법칙을 볼텐데,
join은 단항unary이다.
A. 결합법칙은 어떤 작업(연산)을 어떤 것을 먼저 하느냐가 결과에 영향을 미치지 않는 걸 말합니다. 여기서는, 이항 연산의 작업을 둘로 나눠, “1번 둘을 붙이는 작업”은 이미 있는 상태에서, “2번 둘을 하나로 만드는 작업” 여러번이 순서에 상관 없이 같은 가를 보고 있습니다.
Q. 그냥
join으로 모노이드가 되는 걸 설명하면 될텐데, 왜 굳이 모노이달 카테고리를 언급할까?
A. 이항 연산이 둘로 나뉘어 동작하는 시스템을 보이기 위해, 모노이달 카테고리의 바이펑터가, 모노이드 이항 연산의 “1번: 둘을 붙이는 작업”을 미리 해 놓은 시스템을 만들어야 합니다.
Q. 모노이달 카테고리가 모노이드인가?
A. 둘은 다릅니다. 모노이달 카테고리가 모노이드스런monoidal 성질을 가지지만, 카테시안 카테고리로 만드는 절차도 있고,α,λ,p도 정의해야 되고, 이항 연산이 아닌, 이항 펑터가 동작하므로 구조가 조금 다릅니다. (여기서 모노이드스런 성질은, 제 상상으로 설명하자면, 대상들을 하나의 바이펑터가 들어간 모양으로 모두 표현할 수 있는 것을 의미합니다.)- @todo
Q. 모노이달 카테고리의 모노이드가 추상 대수 모노이드의 일반화인가?
A. Set 카테고리와 바이펑터로 product를 넣으면 추상 대수의 모노이드를 표현할 수 있습니다. -@todo
Q. 왜 모노이달 카테고리의 모노이드가 그리 대단한 대우를 받을까?
A. 함수형은 모노이드 개념이 곳곳에 들어가 있습니다. 모노이달 카테고리의 모노이드는 더 표현력이 늘어나, 원래 모노이드로 볼 수 없었던 것도, 몇 가지 장치로 모노이드로 볼 수 있게 만들어 줍니다. (조금씩은 다르지만, 우리가 어느 정도의 오차를 허용하면 같아 보이는 걸 상상해 볼 수 있습니다.) 예를 들어Maybe a를 받는 곳에Maybe(Maybe a)를 넣을 방법이 생기도록 도와 줍니다.
Q. 모나드를 이해하는데, 모노이달 카테고리를 이해하는 게 도움이 될까?
A. 개인적으론, 이항 연산이 일반화가 되는 걸 본 건, 모나드 이해에도 도움이 됐고, 이를 넘어 모노이드를 보는 눈이 조금 달라졌습니다.