FRAN - Functional Reactive ANimation (스케치 중)

Posted on March 7, 2024

Functional Reactive Animation - Conal Elliott and Paul Hudak, 1997 논문을 본 분들을 대상으로 삼는 글입니다. 무려 27년 전 글이지만, 아직도 많이 읽힌다고 하는데, 검색에는 딱히 걸려드는 한글 자료는 없습니다. 수많은 선행자들이 이해하고 넘어 갔을텐데 자료가 없어 아쉽습니다.

Event와 Behavior 컴비네이션

Reactive를 말로 풀어 설명하면, “이벤트Event가 일어나면 이런 저런 행동Behavior을 한다”입니다. 여기서 일단, Event와 Behavior를 떠올릴 수 있었을테고, 함수형으로 접근하기 위해 이들을 조합하는 방식으로 표현하기 위해 일등급 시민으로 만들고, 컴비네이터들을 설계했을 것이다란 일반적인 상상에서 시작해 보겠습니다.

2.3 Semantics of Events 섹션에 External events 부분에 아래 예시가 나옵니다.

b1 untilB (lbp t0) ==> λe.b2 untilB e -=> b3

untilB :: Behavior α -> Event (Behavior α) -> Behavior α
-=> :: Evant α -> β -> Event β
==> :: Evnet α -> (α -> β) -> Event β

lbp, rbp :: Time -> Event (Event ()) -- 마우스 버튼 누름

결합 순서를 뜻하는 괄호는 없지만, 타입을 고려하면, 아래처럼 해석해야 말이 됩니다.

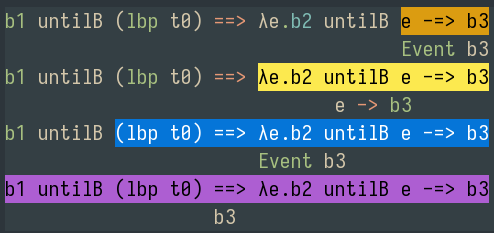
마우스 버튼이 눌리기 전에, 위 체인의 결과는 b1
마우스 버튼이 떼지기 전에, 위 체인의 결과는 b2
마우스 버튼이 떼어진 후에, 위 체인의 결과는 b3

초기 상태가 b1인데, 마우스 버튼을 누르면 b2가 되고, 그 후 버튼을 떼면 b3가 되는 동작을 모델링한 체인입니다.

상상

※ 아래는 FRAN을 해석한다기 보다, 함수형 사고 훈련을 한다는 게 더 맞는 말이겠습니다.

Event가 일어나면 변경되는 값(Event 값)을 보통의 값과 구별없이 취급하는 걸 목표로 혼자 상상해 봤습니다. Event 값을 보통의 값으로 보는 게 아닌, 거꾸로 보통의 값을 Event 값으로 볼 수 있게 하면 둘이 같아졌다 해도 되지 않을까에서 출발합니다.

b1 untilB   (lbp t0) ==> λe. b2 untilB    e -=> b3

lbp t0는 Event (Event α)로 untilB에 그대로 넘길 수 있는 타입이 아닙니다. untilB는 Event (Behavior α)를 받습니다. ==>으로 안에 있는 Event를 변환해야 합니다. 이어지는 ==> λe. b2 untilB e -=> b3를 적용하면, Event는 Behavior타입 b2 혹은 b3로 변환됩니다. 왜 이런 모양으로 컴비네이터를 설계했을까요?

Event가 일어나면 값이 결정될 무언가를, 보통의 값과 같은 것으로 보기 위해, 이 세계의 모든 값은 Event가 일어난 후 값이 결정된다고 가정하겠습니다. Event a가 Event가 일어나면 a를 돌려주는 값이란 뜻입니다. 아무 일도 일어나지 않는 이벤트 I를 정의 하겠습니다. I a는 아무 일도 일어나지 않았을 때 a를 돌려줍니다. 그럼 Event (I a)라고 써도 Event a와 동일합니다. 두 개의 이벤트가 일어나야 값을 돌려준다면, Event (Event a)라고 쓸 수 있다고 금방 상상할 수 있습니다.

순서를 가진 Event들은

Event(Event(Event ...))

모양으로 표현할 수 있습니다. 버튼 떼기는, 버튼 누르기 후 일어납니다. 논문에서는 Event(Event ())로 표현하고 있습니다.

Event는 untilB를 통해서만 값이 될 수 있습니다. 그런데, Event (Event a)는 untilB에 넣어 줄 수 없습니다. 안에 있는 값에 먼저 untilB를 적용해야만, 바깥 Event를 untilB에 넘겨 줄 수 있습니다. fmap으로 안에 있는 Event에 untilB를 적용할 수 있습니다. 인자 순서만 다를 뿐, ==> 의 동작은 fmap과 같습니다. 겹쳐진 이벤트를 처리할 수 있는 방법이 생겼습니다.

안 쪽 Event ()에 untilB를 적용해서 값을 뽑아내면 ()입니다. -=>의 동작은 ==> \_ -> β 동작과 비슷합니다. 그저 Event가 가진 값을 바꿔 놓는 역할을 합니다. 왜 애초에 Event (Event b3)로 lbp를 정의하지 않았을까요? 지금 추측하기엔, lbp를 다른데서도 쓰려면, 지금처럼 placeholder로 ()를 쓰고, 나중에 -=> 로 바꿔놓는 게 더 유연하기 때문이지 않을까 추측하고 있습니다.

아무도 일도 일어나지 않으면 b1,
바깥 Event까지만 일어났다면 b2,
안 쪽 Event까지 일어났다면 b3입니다.

마우스 버튼 누름이 없었다면 b1
마우슨 버튼 누름이 일어났다면, 바로 b2로 결정하는 게 아니라, Event(Event ())중 안에 있는 Event ()를 λe.b2 untilB e -=> b3에 넘겨 줍니다.
e -=> b3로 이벤트e가 가지고 있는 ()를 b3로 바꿉니다.
그 후 Event b3가 아직 일어나지 않았다면, 첫 번째 untilB의 결과(전체 체인의 결과)가 b1대신 b2, 이벤트가 일어났다면 b1대신 b3가 됩니다.

만일 위 의사 코드를 틱(프레임)마다 실행되는 코드로 본다면, 현재 상태가 b2면 바깥쪽 Event는 untilB를 실행하지 않고 바로 안 쪽 Event를 untilB 실행할 수 있어야 합니다.

하스켈로 간단하게 구현한 예

module Main where

data Event a = Event { occurrences :: [(Time, a)] } deriving Show
data Behavior a = Behavior { at :: Time -> a }

type Time = Double
type Position = (Int, Int)

-- 이벤트 시퀀싱을 위한 (==>)
(==>) :: Event a -> (a -> b) -> Event b
Event ex ==> f = Event [(t, f x) | (t, x) <- ex]
-- fmap과 ==>는 인자 순서만 다릅니다.

-- 마우스 클릭과 릴리즈를 Event (Event ())로 모델링
mouseClicks :: Event (Event ())
mouseClicks = Event [
    (0.1, Event [(0.3, ())]),  -- 0.1초에 클릭, 0.3초에 릴리즈
    (0.5, Event [(0.7, ())])   -- 0.5초에 클릭, 0.7초에 릴리즈
  ]

-- 2. 클릭 지속 시간 계산
getDuration :: Event () -> Double
getDuration (Event releases) = 
    case releases of
        ((releaseTime, _):_) -> releaseTime
        [] -> 0

clickDurations :: Event Double
clickDurations = mouseClicks ==> getDuration

-- 특정 시간에 마우스가 눌려있는지 확인
isPressed :: Event (Event ()) -> Time -> Bool
isPressed (Event clicks) currentTime =
    let relevantClicks = takeWhile (\(t, _) -> t <= currentTime) clicks
    in case relevantClicks of
        [] -> False
        xs -> let (clickTime, Event releases) = last xs
             in case takeWhile (\(t, _) -> t <= currentTime) releases of
                    [] -> True  -- 릴리즈가 아직 없음
                    _  -> False -- 릴리즈됨

main :: IO ()
main = do
    putStrLn "\n클릭 지속 시간:"
    print $ occurrences clickDurations
    putStrLn "\n시간별 마우스 상태:"
    mapM_ printState [0.0, 0.2, 0.4, 0.6, 0.8]
  where
    printState t = do
        let pressed = isPressed mouseClicks t
        putStrLn $ "Time " ++ show t ++ "s: " ++ 
                  (if pressed then "Pressed" else "Released")

여기까지 와도 어떻게 보통의 값처럼 쓸 수 있는지 시원하게 정리되지 않습니다.

펑터

https://qfpl.io/posts/reflex/basics/events/ 에 있는 FRP 라이브러리 Reflex의 예시 코드를 보겠습니다.

flipColour :: Colour -> Colour
flipColour Red = Blue
flipColour Blue = Red

eOutput :: Event t Colour
eOutput = flipColour <$> eInput

eInput은 이벤트인데, 보통의 값처럼 쓰는 걸로 보입니다. 어떻게 이렇게 할 수 있을까요? 어찌됐든 a가 아니라 Some a이기 때문에 a에 접근하려면 절차가 필요합니다. eOutput도 이벤트입니다. eOutput에 값을 가져오는 절차를 실행할 때, 내부에 가진 eInput도 처리하게 하면 됩니다.

펑터 절차를 한 번만 하는 게 아니라 내부에 있는 펑터들도 파고 들어가야 합니다. 말보다는 코드가 더 명확히 보입니다.

data Event t a = Event { trigger :: IO (Maybe a) }

instance Functor (Event t) where
  fmap f (Event action) = Event $ do
    result <- action
    pure (fmap f result) -- result 평터 타입의 fmap

이펙트가 있는 action을 실행해서 받은 값에, 한 번 더 펑터 fmap으로 들어가고 있습니다. 펑터가 내부에 또 다른 펑터를 가진 예를 들어보면,

eInput :: Event t Int
eInput = Event $ do
  pure (Just 42)

eOutput :: Event t String
eOutput = show <$> eInput -- eInput이 마치 일반 값처럼 보입니다.

Event의 fmap은 Event를 뚫고 들어가, 내부 펑터(여기선 Just)도 뚫고 들어가게 구현되어 있습니다.

Q. 일반 값처럼 쓸 수 있냐를 보는데, 왜 펑터로 함수를 적용하는 것을 보나요?
A. 값이 필요한 시점은 함수가 필요로 할 때 말고는 없습니다. 일반 값처럼 쓴다는 말은, 함수가 필요로 할 때, 프로그래머가 최대한 신경을 덜 쓰게 한다는 말입니다.

어차피 나중에 아래같은 runEvent를 걸테니

runEvent :: Event t a -> IO ()
runEvent (Event action) = do
  result <- action
  case result of
    Just val -> putStrLn $ "Event값: " ++ show val
    Nothing -> pure ()

main :: IO ()
main = do
  runEvent eOutput

코드 동작이 일반 값과 같다는 얘기가 아니라, 프로그래머 입장에선 신경쓰는 정도가 일반 값과 다르지 않다는 얘기입니다. eOutput은 eInput을 기반으로 구현되어 있는데, eInput이 가진 값을 가져오는 것은 신경쓸 필요가 없어졌습니다.

특별한 얘기가 없습니다. 모두 평범한 펑터 타입에 관한 얘기입니다. a가 아니라 Some a는 언젠가 Some에 맞는 어떤 작업을 하겠다는 계산 약속입니다.

펑터의 <$>는 $의 일반화 버전으로 볼 수 있습니다. 값에 함수를 적용한다는 것의 추상화입니다. Event가 보통의 값처럼 보이는 이유는, 내부 구조를 신경쓰지 않고 함수를 적용할 수 있기 때문입니다.

Push or Pull

일이 일어난 쪽에서, 청자에게 알려 주든가,
청자가(혹은 제3자가) 계속 일이 일어났는지 물어 보든가

두 가지 방법뿐이 없습니다.

일등급 시민으로 타입(Event,Behavior)을 설계하고 그냥 함수로 일반 값 다루듯이 하는 게 언뜻 이해가지 않았습니다. 아마도 옵저버블 패턴(리스너 패턴) 자체가 어떻게 함수형으로 구현되는지 너무 일찍 궁금해 해서 그런 듯 합니다. 위 untilB 체인은 프레임(틱)마다 계속 실행하는 걸로 생각하고 읽으면 됩니다. 리스너를 쓰지 않는다는 말이 아닙니다. 나중 외부 이벤트와 붙이게 되면, 리스너를 써야만 합니다. 논문에서 구현 전에 나오는 내용은 리스너와 붙이는 것을 대체하는 게 아닌, 리스너로 통지를 받은 후에 전파되는, 일종의 이벤트 네트워크를 표현하는 방식에 관한 얘깁니다.

Event 타입은 특별한 동작이 있습니다. Event가 발생하기 전엔 코드가 진행되지 않게 막을, 블록할 방법이 필요합니다. FRAN에선 바로 언급하지 않고 있지만, 저는 구현을 생각하며 쫓아가는 게 이해하기 편했습니다. 구현에선

Event값이 Just인지 Nothing인지 봐서, Nothing이면 더 이상 코드 진행을 하지 않고 끝내거나,
Event값이 MVar나 IORef등으로, 자체적으로 값이 생길 때까지 블록하는 능력을 쓰는 방법이 있겠습니다.

첫 번째 방법을 pull, 두 번째 방법을 push로 부르는 것 같습니다. push 방법은 바로 전체 체인의 결과가 바로 나오는 게 아니니, 체인 중간 중간 결과가 의미있게 드러난다면 가능할 것으로 보입니다. 어차피 MVar나 IORef를 써야하니, 이펙트에 의미를 잘 심으면 될 것으로 보입니다.

Denotational

수학으로 코드의 동작을 예측할 수 있어야 한다는데, 이 부분은 넘어가겠습니다.

시간 연속 Continuous

FRAN 논문의 2.1 Semantic Domains

아래는 추측입니다.

pull로 구현한 상황을 보겠습니다. Event가 3.5초에 일어났다고 보겠습니다. 0.5초 단위로 샘플링하고 있었다면, 이 이벤트는 정상적으로 캡처됐겠지만, 만일 1초 단위로 샘플링하면 3초에 샘플링할 때도 이 값은 없고, 4초에 샘플링할 때도 이 값은 없습니다. 이 Event를 놓치지 않는 방법을 생각해 봤습니다.

이벤트를 스트림에 담아 둡니다. 4초에 샘플링을 할 때 볼 수 있어야 합니다.
FRAN에선 애초에 의미를 3.5초가 아니라, 3.5초 이상에 일어났다고 정의하고 있습니다. 항상 3.5초보다 큰 다음 샘플링 시각이 최상위 값입니다.

이렇게 정의하면 샘플링 단위 시간에 상관없이 이벤트를 놓치지 않을 수 있습니다. 벡터 그래픽을 비트맵으로 만드는 것과 비슷한데, 너무 일찍 비트맵으로 만들어 버리면 데이터를 잃어버리는 양이 늘어 나듯이, 최대한 시각이 아닌, 시간, 즉 범위로 정보를 끌고 다녀야 합니다.

샘플링에 상관없이 결과를 내려면, 확정된 하나의 값이 아닌, 최대한 범위로 정보를 들고 다녀야 합니다. 이렇게 하기 위해 논문에선, 시간을 집합론의 Order Theory로 정의하고 있습니다.

1 ⊑ 2 ⊑ 3.5이상 ⊑ 4

3.5 이상이면 4일지 더 큰 수일지 알지 못하지 않나 싶은데, 위 처럼 순서가 나오도록 다음과 같이 정의해 놨습니다.

x ≤ y이상 if x ≤ y
x이상 ≤ y 는 undefined
x이상 ≤ y이상 undefined

처음 볼 때 금방 이해가 안갔습니다. x이상, y이상을 하나의 수처럼 바라보긴 하는데, x이상이 y보다 작을지 클지는 모른다는 직관 그대로 undeinfed라 정의해놨습니다. denotational한 의미를 정의하는데 중요한 역할을 하는 정의라고 하는데, 천재적인 것 같기도 하고, 말장난 같기도 합니다. 어쨌든 시간의 크기보단 순서가 의미가 있다 정도로 넘어갔습니다.

⊑는 크기가 작다는 뜻이 아닙니다.(이름은 Square Image of or Equal To 라 부르는 기호입니다.) 순서상으로 먼저와 나중을 표현하는 기호입니다. 3.5는 4보다 작지 않을지 몰라도 순서상으론 앞에 오도록 약속, 규칙을 정의합니다. 만일 샘플링을 0.2초 단위로 한다면 3.5는 3.6보다는 (작은 게 아니라) 먼저라는 뜻입니다. “어떤 수 이상”이란 원소들은 자신이 속한 샘플링 구간을 넘지 않는다는 약속이니, 어떤 샘플링 단위에서도 정보를 잃어버리지 않는다로 이해하고 있습니다.

현재 구현된 FRP 프레임워크들 중에 퍼포먼스도 잘 나오고, Continuous 시간도 이론대로 구현한, 두 마리 토끼를 다 잡은 프레임워크는 없다는 것 같습니다. 코널 엘리엇 교수의 여기 저기 글을 보면, FRP는 denotational하고, Continuous 시간을 표현, 구현해야 제대로 FRP라 할 수 있는데, 그런 의미에선 아직은 제대로 실용 가능한 퍼포먼스를 보이는, 원론을 그대로 구현한 FRP프레임워크는 없다는 뜻입니다. 물론 적절한 선에서 타협한 실용 라이브러리들이 여럿 있습니다.

외부 이벤트와 연결 구현 예시

{-# LANGUAGE RecursiveDo #-}

import Control.Monad.Fix (MonadFix)
import Control.Monad (forever)

-- Event 타입 정의
newtype Event a = Event { runEvent :: IO (Maybe a) }

-- Event를 실행하고 결과를 반환하는 함수
triggerEvent :: Show a => Event a -> IO ()
triggerEvent (Event action) = do
  result <- action
  case result of
    Just val -> putStrLn $ "Event triggered with value: " ++ show val
    Nothing  -> putStrLn "No event occurred"

-- 단순히 값을 가진 이벤트를 생성
pureEvent :: a -> Event a
pureEvent val = Event $ pure (Just val)

-- 입력 이벤트를 시뮬레이션
inputEvent :: Event Int
inputEvent = Event $ do
  putStrLn "Enter a number (or empty to skip):"
  input <- getLine
  if null input
    then pure Nothing
    else pure (Just (read input))

-- 이벤트 변환
mapEvent :: (a -> b) -> Event a -> Event b
mapEvent f (Event action) = Event $ do
  result <- action
  pure (fmap f result)

-- 실행 루프
eventLoop :: Show a => [Event a] -> IO ()
eventLoop events = forever $ mapM_ triggerEvent events

-- 예제 실행
main :: IO ()
main = do
  -- 두 이벤트 정의
  let e1 = inputEvent
  let e2 = mapEvent (\x -> x * 2) e1 -- 입력 값을 2배로 변환

  -- 실행 루프
  eventLoop [e1, e2]

Github 계정이 없는 분은 메일로 보내주세요. lionhairdino at gmail.com