주의 - 아래 내용은 유사 수학이란 지적을 들은 적이 있습니다. 여기 설명이 어떤 분들이 보기에는 유사 수학일 수 있습니다. 애초에, 수학적인 의미보다는 개념이 가지고 있는 어떤 아이디어가 프로그래밍에, 하스켈에 녹아든 건지 찾는 게 목표로, 굳이 유사 수학이 아니라고 밀어 붙이진 않겠습니다. 주제는 수학에서 가져온 것이지만, 수학적인 의미를 찾는 분들을 위한 글이 아닙니다. 아마도 수학 전공이나, PL 전공분들이 보기에 적당하지 않은 상상, 그리고 당연히 오류가 있을 수 있습니다.
현재의 제 수학 배경으론 완벽히 이해하기엔 무리가 있지만, 적정선까지 이해를 하면, 함수형 프로그래밍으로 현실을 모델링할 때 분명 힘이 될 개념이라 생각합니다. 하스켈 프로그램은 하나의 거대한 모노이드로 만들어지니, 무언가를 같거나, 조금 다른 걸 우겨서라도 같다고 보는 테크닉이 중요합니다. 모나드는 (이펙트가 추가 되며) 조금 달라진 걸 원래의 것과 같게 볼 수 있는 방법에 대한 얘기였습니다. Adjunction도 두 개의 무언가가 얼마나 같은 가를 포멀하게 얘기하는 하나의 방법입니다. 둘이 연관성이 있을 거라 예측할 수 있습니다. 참고 - 모나드, 같음 - m (m a)와 m a는 얼마나 다를까?
카테고리 이론에 대한 글을 남기는 건, 어설퍼서 잘 안하는데, 재미난 상상이 떠올라 남깁니다. 아래가 궁금하지 않은 분들은 읽을만한 글이 아닙니다. 항등, 동형, 펑터, 자연 변환에 대해 간단히 짚고 가긴 하지만, 부족한 설명들이니, 다른 정식 텍스트들을 통해 제대로 알아두시면 좋습니다.
ϵ과 η의 화살표 방향이 반대일까?=을 쓸만큼 같지 않으면 ~도 쓰고, ≃, ⋍, ≅, …(=과 여러 기호의 조합)을 써서 그래도 어찌 보면, 어느 정도는 같게 볼 수 있다고 말하는 개념들이 많습니다. Adjunction도 그들 중 하나입니다.
다시 한 번 말하지만, 수학 카테고리 이론의 Adjunction을 정교하게 공부하려는 분에게 어울리는 글이 아닙니다.
@todo: 영어 용어와 우리말 용어가 마구잡이로 섞여있다. 한 쪽으로 통일해야 하지 않을까?
모나드를 해석하면서, 이펙트가 섞여 있는 것들 타입을 맞춰 나가는 훈련을 했으니, “같다”는 개념에 약간의 지식이 생겼겠지 하고 붙었습니다. 하지만, 동형, 자연 변환 등의 기본 용어 조차, 어렵사리 어떤 동작을 하는지만 알지, 의미를 충분히 알지 못하고 있구나를 느꼈습니다. 역시, “같다”는 개념은 어려운 주제 같습니다.
F∘G = , ~=, -> id_D
G∘F = , ~=, -> id_C (나중에 얘기하겠지만, 이건 ->는 안되고 <-여야 합니다.) 위에 식 중 어떤 걸 만족하냐에 따라 C와 D의 조금씩 다른 관계를 표현할 수 있습니다. 여기에 숨은 뜻을 보기 위해 아래 질문들을 먼저 고민해 봤습니다.
isomorphic인 것과 homomorphic 중 isomorphic이 아닌 것들의 차이는 뭘까요? 구조는 유지하며 변환해 갔지만, 다시 처음으로 돌아오지 못한다입니다.(역연산이 존재하지 않음) 어떤 경우에 처음으로 돌아오지 못할까요? collapse 됐다거나, 새로운 뭔가가 추가 됐다거나 해서 처음 정보를 잃어버리거나 관계 없는 경우에 돌아 갈 수 없지 않을까 추측하고 있습니다. 처음을 잃어버려도 필요한 정보는 살아 있는 가장 간단한 경우를 예를 들면, 0포함 자연수들에서 1+2의 결과로 3을 받았을 때, 3만 보고선 1+2의 결과인지 1+1+1, 3+0, …인지 알 수 없습니다. 하지만, 필요한 정보는 3이기 때문에 처음 출발지를 잃어버려도 상관없습니다. Writer 모나드의 로그 누적을 보면 "this is log"에서 "this is"가 먼저 쌓였는지 "this"가 먼저 쌓였는지 알 수 없습니다. 하지만 필요한 건 최종 전체 로그이니, 어떻게 쌓였는지 몰라도 상관없습니다. Reader 모나드의 경우 외부 스코프의 상수값을 두 번 읽어오나, 한 번 읽어오나 차이가 없으니, 몇 번을 읽었는지 알 필요가 없습니다. Maybe의 경우 기존에 없던 Nothing이 추가 되어 돌아갈 수 없습니다. 세상엔 이 정도로만 같으면, 이 정도의 관계만 있으면 되는 경우가 무수히 많습니다.
id와 자연 동형인 것과, id로 변환해주는(처럼 볼 수 있게 해주는) 자연 변환이 있는 것의 차이가 뭘까요?
카테고리가 동형인가를 알아보려면, 둘 사이에 id펑터 역할을 할 수 있는 펑터 조합이 있는가를 봅니다.
펑터 조합이 id펑터와 동형인지 보려면, 자연 동형인가를 알아봅니다.(만일 없다면, 여기서 제약을 조금 낮춰 자연 동형과 비슷하게 볼 수 있는 방법을 찾는데, 방법이 찾아지면 동형 관계는 아니지만, 그보다는 좀 약한 Adjunction이 (펑터가) 있는 관계라 합니다.)
그럼, 자연 변환이 동형인가를 보려면? 계속 뎁스가 들어가며 관계를 보면, 무한히 관계를 표현하는 개념이 나와야 될 것 같지만, 자연 변환 동형은 자연 동형을 이루는 각 성분들이 모두 동형인가를 봅니다.
카테고리에선 대상 언급 없이 모든 걸 풀어나가니, 같음도 마찬가지로, 대상을 보지 않고 정의합니다. 모피즘이 되는 것들이 id 모피즘과 같아지는지, 동형과 같거나 비슷하게 만들 방법이 있는지 등을 찾아 봅니다.
모르는 것 투성이라 글로 정리하는 게 의미있을까 싶어 계속 미루고 있었는데, 약간 기록할만한 상상이 생겨 정리했습니다.
얼마나 같은가란 말이 이상하지 않나요? 같으면 같고, 다르면 다르지, 어느 정도 같다는 건 그냥 다르다란 말 아닌가요? 다르지만, 일부가 같다면, 아예 전부 다른 것과는 별도로 써먹을데가 있습니다. 가진 정보가 두 가지인데, 이 중 하나는 같고, 다른 하나는 다르다면, 둘 다 다른 것과는 달리 볼 수 있습니다.
비유하자면, 10가지 정보가 모두 같으면 동형,
필요한 9개는 다 같고, 관심 없는 나머지 1개는 같은지 다른지 관심 없으면 준동형,
필요한 9개 중 8개는 같고, 하나는 다르면 Adjunctions 관계의 펑터가 있는 관계
이런 느낌입니다. 그래도 10개 중 8개는 같으니, 닮았다 할 수 있고, 아예 다른 것과는 다르니 이 걸 위한 형식화를 해보자 같습니다. 너무 둘이 다르면 의미가 없는 경우가 많습니다. 어디까지나 비유입니다.
Ad(무엇과 가까이, 어디를 향해, 무엇과 관련하여) - Joint(jungere 결합하다)
Ad - Junction “closely connected, joined, united”를 뜻하는 라틴어 Adjunction
일상 생활에서도 가끔 영어 자체로 만나는 용어입니다. 고속도로와 고속도로가 만나서, 한 고속도로에서 다른 고속도로로 옮겨 갈 수 있는 연결 지점을 Junction(JC, 우리말로는 분기점)이라 부릅니다. Ad는 보통 도움을 주는것에 붙입니다. verb, adverb 처럼요. Adjunction은 연결을 도와주는 무언가일거라 상상하면 되겠습니다.
Adjoint 용어를, 무슨 뜻으로 붙인 건지 명확하게 정의하는 곳은 못 찾았습니다. 보통 둘이 특별한 관계가 있다는, 매우 추상적인 설명으로 (불친절하게) 끝나는 자료가 대부분입니다. (안하니만 못한 말 같은 이런 말로 용어 사용을 설명하다니!) 거의 같은 말이지만, 조금 더 구체적인 느낌을 주게 말하자면, 적당한 펑터 짝을 고르면, 자연 변환 두 가지를 동원해 두 카테고리를 꽤 닮은 꼴로 만들 수 있을 때, 각 각을 오른 쪽, 왼 쪽 Adjoint 펑터라 하고, 연결을 도와주는 자연 변환 두 가지와 합쳐 Adjunction이라 부릅니다. 두 카테고리 사이에 Adjunction을 두면 isomorphic보단 약하지만, 어찌 보면 그런대로 같다고 볼 수 있게 됩니다. 카테고리를 오가게 하는 두 펑터를 합친다고 딱 Isomorphism이 되는 건 아닌데, 그렇다고 관계가 별로 없다고 보기엔, 적당한 상황에선 Isomorphism과 비슷한 걸로 만드는 역할을 하니 붙일 이름이 필요하지 않았을까 싶습니다. 하나의 카테고리를 다른 카테고리와 (isomorphic보단 덜하지만) 강하게 연결할 때 쓰는 무언가입니다.
둘이 같다를 둘이 연결junction할 수 있다는 메타포로 바라보면 수긍가는 용어입니다. 서로 다른 크기의 파이프 둘을 연결할 때 쓰는 커넥터입니다.
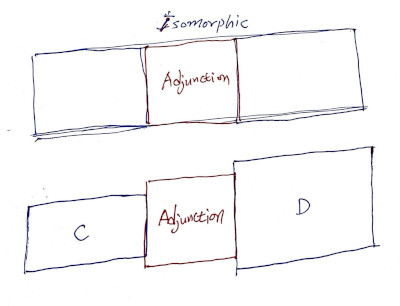
※ 명사냐 형용사냐로 갈릴 뿐, Adjoint와 Adjunction은 뜻 자체는 거의 같은 뜻으로 쓰입니다.
아래 용어들은 몇 번을 봤던 개념들인데, 다 알고 있다 생각했는데, 의외로 혼란스러운 부분이 많았습니다. 항등원은 어떤 연산에 대해서 정의되는데, 항등 함수와 항등 펑터, 항등 자연 변환들은 어떤 “연산”에 대해 정의된 것인가부터, 텍스트마다 F, id_F를 펑터, 항등 펑터, 항등 자연 변환 표현으로 혼용해서 쓰는 바람에 더 혼란스러웠습니다. 항등 뭐뭐들은 정의와 성질을 혼동하기도 했습니다. 정식 정의들이 아니라 Adjunction을 이해하는데 필요한 아이디어만 정리했습니다.
Adjunction 정의 방법이, universal morphisms을 쓰는 것, Hom-set을 쓰는 것, counit-unit을 쓰는 것 세 가지가 있는데, 여기서는 세 번째 counit-unit 으로 정의하는 걸 뜯어 봅니다.
추측 - 둘이 같다, 둘이 isomorphic하다, 둘이 Adjunction이다.. 식으로 쓰나 했는데, Adjunction은 두 카테고리가 사이에 두어, 두 카테고리를 연결할 때 도와주는 도구 같은 겁니다.
두 카테고리는 Isomorphism이 있는 Isomorphic 관계
두 카테고리는 Adjunction이 있는 ~ 관계 -- 따로 ~에 들어가는 용어는 없나 봅니다.식으로 말하면 되는 듯 합니다.
카테고리에선 대상을 매핑하는 동작은 모피즘, 카테고리를 매핑하는 동작은 펑터라 부릅니다. 함수가 한 가지만 매핑한다면, 펑터는 오브젝트도, 모피즘도, 모피즘 합성도 모두 매핑(카테고리를 매핑)해야 합니다. 참고 - 한 번쯤 나올 법 했는데, 아직 없었던 펑터 이야기
텍스트들의 설명으론, > “구조가 같은 두 대상” 사이에서 “모든 구조를 보존하는 사상”을 isomorphism이라 합니다.
개인적으론 매우 마음에 들지 않는 설명입니다. 이미 구조가 같은 대상이라 얘기했는데, 그럼 보존됐다고 보는 게 당연한, 같은 말을 두 번 한 듯한 문장입니다. 전체 구조는 다른데, A가 가진 구조와 동일한 구조가 B에 있으면 Homomorphic이라 합니다. 전체 구조까지 같아서 이름만 다를 뿐, 같은 것으로 볼 수 있는 건 isomorphic이라 합니다. 둘이 전체 구조가 다르더라도, 둘을 일대일 대응으로 오갈 수 있게 해주는 isomorphism이 있으면(upto isomorphism), isomorphic이라고 말합니다.
한 시스템에서 어떤 상태가 어디에서 출발해서 어떤, 어떤 값을 거쳐 어디에 도달하는 상황을 생각하면, 이를 모델링한 곳에서도 항상 동일한 경로로 변경이 되어, 모델링 한 것으로 현실을 완벽히 추적할 수도 있고, 거꾸로 현실에서 모델링한 것이 어떻게 값이 변해갈지 완벽히 추적할 수 있는 걸 말합니다. 두 시스템의 상태가 완전히 일대일 대응으로 어느 한 쪽을 알면, 다른 한 쪽도 알 수 있는 iso(같은)morphic(모양)이라 합니다.
homo- 는 same을 의미하고, iso-는 equal을 의미한다고 합니다.
same은 identity를 보는 것이고, equal은 equality를 본다고 합니다. 동어 반복 같은 설명입니다.
“today’s exchange rate 1 dollar is equal to 0.91 euros. but they are not the same thing”
구글링으로 여러 설명을 찾아 봐도 딱히 명쾌하단 느낌을 주는 설명이 없습니다.
대수에선 위 예문과 좀 다른듯 한데, 제 경험적으로 느끼는 건, 내가 주목하는, 필요로하는 구조는 같고, 그 외는 같을 수도, 다를 수도 있는 (거의 비슷한) 것에는 homo-를 붙이고, 모든 구조가 같아 일대일 대응이 되어 (역변환이 되는 것) 서로 바꿔칠 수 있는 것, 이름만 다르지 전혀 구별할 수 없는 것에는 iso-를 붙입니다. 물론 “upto isomorphism”일 때 얘깁니다.
어떤 연산에 항등원Identity(Element)이라면, 항등원과 연산하면 원래 값이 바뀌지 않는, 다른 말로 하면 해당 연산과 만났을 때 아무 일도 일어나지 않는 걸 항등원이라 합니다. 대수학 정의를 보면
e_L * a = a 이 성립하면 좌항등원
a * e_R = a 이 성립하면 우항등원
이 둘이 모두 성립하면 그제서야 항등원이라 합니다. (추가적으로 따라야 하는 법칙들이 몇 개 있습니다.)
참고 - 결합 법칙, 교환 법칙, 항등원, 합성
※ 잡소리 - 연산은 인자만큼 대상을 변환하는데, 어떤 인자로 변환을 시도했더니 변환되지 않더라에서, 이 인자를 연산의 고유한 특성을 가리키는 “Identity”로 부르고 있습니다. 수많은 연산 중에, 이 연산을 가리킬 수 있는 고유 특성이 될까요? 0이라는 Identity를 가진 연산은 +뿐이 없는 걸까요? 자연수에 연산을 적용한 걸 각각 나눈다면, 여기 팀은 0+0+0, 0+1+0, 0+2+0… 모두 이 모양을 가지고 있습니다. 이 팀의 Identity는 0+ +0이라는 뜻일까요?
id_X: X -> X
모양은 X를 넣어주면 변형, 변환 없이 그대로 X가 나오는 함수입니다. 정식 정의는 다른 텍스트들을 참고해 주시고, 제가 눈여겨 보는 것은 다음 성질입니다.
좌항등원, 우항등원처럼 임의의 함수 f: X -> Y와 합성(⋅)이라는 연산에 대해
f ⋅ id_X = f
id_Y ⋅ f = f
성질을 만족해야 합니다. 잘 보면 id_X와 id_Y 두 가지가 나옵니다. 단일 값인 1같은 값의 더하기 연산에 대한 항등원은 1 + 0 = 0, 0 + 1 = 0 으로 하나의 값인 0이 항등원이었지만, 함수는 한 가지 정보를 가지고 있는 값이 아닙니다. 두 가지 정보 X, Y를 갖고 있는 X -> Y란 함수의, 함수 합성(연산)에 대한 항등원 역할을 하는 건, 두 가지를 봐야 한다고 예측할 수 있습니다. 시작점과 끝점이 있는(방향이 존재하는) 것의 좌항등원, 우항등원을 봐야 하니, 두 가지가 나올 수 밖에 없습니다.
만일 f: X -> Y 함수라면,
f ⋅ id_X를 하려면 id_X: X -> X 타입일테고,
id_Y ⋅ f를 하려면 id_Y: Y -> Y 타입이 되어야 합성 할 수 있습니다.
타입 일치를 보면서, 그냥 당연하다고 넘어가면 되겠지만, 전 두 가지 정보가 있는 것의 연산에서 항등원은 두 가지를 봐야 한다는 것에 눈이 갔습니다. 하스켈에서는 폴리모픽으로 정의해서 id :: a -> a 하나로 표현만 할 수 있지만, (⋅) 연산에 대해 항등 함수 성질을 만족하려면 id_X, id_Y 두 개의 항등 함수가 있어야 합니다.
Identity 펑터는 뭘 의미할까요? (Identity 모피즘과 구별) 어떤 연산에 Identity라는 걸까요?
함수가 함수 합성이란 연산에 대해 항등원을 찾았듯이, 펑터 합성 (∘)에 대한 항등원입니다. 함수 합성 (⋅)과 구별하기 위해 속이 빈 동그라미로 표기하겠습니다.
카테고리 C, D가 있을 때
정의는 id_C: C -> C 모양에 C에 있는 모든 대상X에 대해 id_C(X) = X 이고, 모든 모피즘 f에 대해 id_C(f) = f 이고,
펑터 F와 합성해서 다음을 성질을 만족하면
F: C -> D
id_D ∘ F = F = F ∘ id_C
id_C, id_D 들을 항등 펑터라 합니다. 항등 성질을 찾을 때, 좌 우를 봐야 하니 자연히 두 가지가 나옵니다.
어설프게 펑터, 항등원, 항등 함수를 차례로 짚으면서 온 이유가, 어떤식으로든 펑터로 항상 같음(항등)을 말하려면 두 가지 정보가 필요하다는 걸 보기 위해서입니다.
어떤 타입의 대상이 작업(펑터)을 거친 후에도 같은 타입으로 돌아 오는 모노이드로 만들려면, 원래부터 같다는 개념 자체가 두 가지 정보를 필요로 하고, 펑터 두 개로 표현할 수 있는 게 당연하다로 이어지는 상상입니다. 다 작성한 후에, 아 잘 못 생각했구나 라고 할 수도 있는, 아직까지는 그저 상상입니다.
F: C -> D
G: C -> D
두 펑터를 매핑하는 η: F -> G(혹은 두 줄 화살표 η: F => G)를 자연 변환이라 합니다. ()펑터는 대상과 모피즘을 모두 매핑하는 동작을 가지고 있습니다. 이런 동작을 가진 작업 둘을 매핑하므로, 한 가지 정보들을 매핑하는 함수와는 달리 다음 성질을 추가적으로 만족합니다.
X, Y는 카테고리 C의 대상object, f: X -> Y는 모피즘
F(X) --- F(f) ---> F(Y)
| |
η_x η_y
| |
V V
G(X) --- G(f) ---> G(Y)(@todo: 그림으로 대체할 것)
η_y⋅F(f) = G(f)⋅η_x말로 풀면(상상하면) 자연 변환은 두 펑터가 얼마나 다른가를 나타내는 모피즘입니다.
F로 변경한 F(f)를 적용하고, η로 보정한 것과
η보정을 먼저하고, G로 변경한 G(f)를 적용한 것이 같습니다.
상상 - 하나의 f를 변형해서 F(f)와 G(f) 만들었을 때, 둘은 어떤 관계가 있을까요? 최종 결과값 F(Y)와 G(Y)를 봐서는 별다른 관계가 없어 보이지만, 한 뿌리(f)를 변형한 두 가지(펑터의 결과)는 어떤식으로든 관계가 있지 않을까요?
자연 변환이 앞뒤로 붙는 걸 유심히 봐 둬야 합니다. 펑터는 함수와 마찬가지로 정의역domain, 치역codomain 두 가지 정보를 가지고 있습니다. 이렇게 시작과 끝이 있는 걸, 얼마나 다른지 보려면, 출발지는 얼마나 다른지, 도착지는 얼마나 다른지 두 가지를 봐야 합니다. 위 식은
“F(f)를 적용하고, 도착지를 수정한 것 = 출발지를 수정하고 G(f)를 적용한 것”
을 나타냅니다.
여기에 짚고 넘어가야 하는 뜻이 있습니다. 만일 F의 공역과, G의 공역이 같고, F(f)에 대응하는 G(f)가 반드시 있어야 가환할 수 있습니다. 자연 변환의 대상이 되는 두 펑터는 공역이 같아야 합니다. 나중 화살표가 뒤집어진 이유를 볼 때 필요합니다.
F(X)에서 G(Y)로 가는 모피즘은 두가지가 나왔습니다.
η_y∘F(f)G(f)∘η_x두 개의 결과는 같습니다. 여기엔 재밌는 직관이 있습니다. 단순하게 a->b 모피즘을 a에서부터 거리를 재는 것과 비유해 보겠습니다. 대상의
결과가 같다는 말과 비슷합니다. 원래부터 거리를 잰다는 행동에는 기준점을 정하는 것부터 시작인 걸 생각해 보면, 당연한 결과입니다. 다시 말해, 거리를 재는 행동, 즉 a->b 모피즘은 기준점 a를 옮겨서 b로 간 경우와, a는 그대로 두고 b를 옮긴 경우가 같은 동작일 경우가 나올 수 밖에 없습니다. 모든 숫자는 0에서부터 거리를 잰 값입니다. 1은 0->1, 2는 0->2… 로 볼 수 있다는 말입니다. 세상의 모든 값은 사실은 컴퓨테이션으로 볼 수 있다라고 해서 좋은 소리를 못들은 적이 있는데요. 자연 변환이 하는 얘기가 이 말이 아닌가 조심스럽게 남겨 봅니다. 모든 대상을 비교할 때는 기준점부터 같은가를 확인하고, 같은 기준점에서 같은 거리에 있는가를 봐야지 같다고 말할 수 있습니다. 기준점, 떨어진 거리, 방향 이렇게 3가지가 맞아야지만 “같다”라고 얘기할 수 있습니다.
@todo 아직은 Adjunction의 두 자연 변환이 화살표가 뒤집어진 이유에 대한 직관에 도달하기엔 좀 미흡하다.
※ 펑터가 대상이 되는 펑터 카테고리에선 모피즘이 자연변환입니다.
※ 같은 둘의 자연 변환을 보겠습니다.
F(X) --- F(f) ---> F(Y)
| |
id_X id_Y
| |
V V
F(X) --- F(f) ---> F(Y)id_Y∘F(f) = F(f)∘id_X가 나왔습니다.
X->Y의 항등 함수를 볼 때, 나왔던 식입니다.
id_X ----> F(f) ----> id_Y모피즘은 강조했듯이 한가지 정보가 아닙니다. a->b는 a, b 그리고 -> 방향까지 세가지의 정보가 있습니다. 이들이 같은가 볼 때는 역시 세 가지를 모두 봐야 합니다.
id_X,id_Y, 합성∘ 순서
조금 억지스럽지만, 기준점을 확인(id)하고, 거리를 재든, 거리를 재고 기준점을 확인하든 차이가 없다는 얘깁니다.
모피즘의 비교에 있어 정말 잘 만든 표현 방법 같습니다.
카테고리 C, D
펑터 F: C -> D
항등 자연 변환 id_F(F) -> F
펑터 F를 변환해도 F가 나오는 자연 변환입니다. 항등 자연 변환도 역시 왼 쪽, 오른 쪽을 봐야 합니다.
※ 텍스트들이 id_F가 자연 변환인지, 펑터인지 딱 짚어서 말해주지 않는 경우가 많습니다. 심지어 그냥 F로 쓰고 자연 변환을 뜻할 때도 있고, 항등 자연 변환을 뜻할 때도 있습니다. 알아서 잘 보는 수밖에 없다고 합니다.
위의 자연 변환 가환 다이아그램에서 자연 변환 η의 동작을 보면, 시작지를 변형하는 η_x와, 도착지를 변형하는 η_y가 따로 있습니다. 이들 각 각이 모두 역 매핑이 존재한다면, 즉 η_x_inverse , η_y_inverse가 있어, η의 모든 “성분component”들이 isomorphic일 때, 자연 동형이라 합니다. 이럴 때 η를 isomorphism of functors라고도 부릅니다.
F와 G는 다르지만, η가 있으면 F와 G는 구별할 수 없는 “같은” 펑터입니다.
이제 슬 본론으로 들어갈 준비를 마친 것 같습니다. 위 용어 설명들은 텍스트에 나오는 정확한 내용들이 아니라 조금씩 상상이 들어가 있습니다. Adjunction에서 같음 개념을 볼 때,
왜 F, G 두 펑터의 합성을 들여다 보는지,
F∘G = id_D가 아니고, G∘F = id_C가 아니라서, F와 G의 합성 F∘G와 G∘F가 isomorphism 역할을 못 한다면,
ϵ(F∘G) = id_D와 η(G∘F) = id_C 있으면 될 것 같은데, 왜 G∘F = η(id_C)가 있는지 보기 위한 사전 생각 스트레칭들입니다.
※ 여기서는 Adjunction을 만드는 두 Adjoint 펑터가 만나서 모나드가 되는 것만 보려고 합니다. 결론부터 말하면, Adjunction도 결국 얼마나 같게 볼 수 있는가에 관한 얘기입니다.
우리말 번역으론 “수반 함자”라고 합니다. 隨伴 따를 수, 짝 반 : 어떤 사물 현상에 따라서 함께 생기는 것. 안타깝게도 전 번역이 딱히 더 익숙하지도, 더 구체적인 감을 주지도 않습니다.
C,D는 카테고리, F,G는 펑터
F: C -> D
G: D -> CF∘G = id_D이고, G∘F = id_C이면 카테고리C와 카테고리D는 동형isomorphic입니다. 조금 더 풀어서 얘기하면, 어딘가의 펑터 합성식에 id_D가 등장한다면, 아무런 추가 작업 없이 그냥 F∘G를 쓸 수 있습니다. 그런데, 현실에선 이렇게 딱 동형이 아닐 때도 의미가 있는 경우가 많습니다. Adjunction은 딱 동형은 아니지만 어찌 어찌하면 동형처럼 보일 때에 관한 얘기입니다.
F와 G를 써서 Adjunction을 만들려면 필요한 (ϵ, η)는 다음과 같은 두 개의 자연 변환Natural Transformation으로 이루어진 순서쌍이라고 합니다.
epsilon ϵ: F∘G => id_D
eta η: id_C => G∘F여기까지가 보통 텍스트들 서두에서 볼 수 있는 내용입니다. 참고-Wiki - Adjoint Functor. 당연하게도 비수학인이 봐서 이해할만한 자료는 거의 없습니다. 이제부터는 대부분 제 상상입니다.
상상해보면, ϵ, η가 없으면 F∘G를 id_D처럼, id_C를 G∘F처럼 볼 수 없지만, ϵ, η의 도움을 받으면(보정한다면) F와 G의 합성으로 id_D, id_C와 같은 일을 할 수 있습니다.
F∘G가 id_D가 아닌데, ϵ으로 살짝 보정하면 id_D 동작을 하고,
G∘F가 id_C가 아닌데, η로 살짝 보정하면 id_C 동작을 한다고
보면 순조롭게 넘어 갈 수 있을 것만 같습니다.
하지만, η가 화살표 방향이 반대입니다. G∘F를 주면 id_C를 돌려주는 게 아니라, id_C를 주면 G∘F를 돌려줍니다.
만일
F∘G가 아무 조치 없이 id_D가 되고,
G∘F가 아무 조치 없이 id_C가 되면
카테고리 C와 D는 isomorphic합니다.
C와 D가 딱 isomorphic하진 않지만,
F∘G가 id_D와 같지 않은데, F∘G ~= id_D가 있고,
G∘F가 id_C와 같지 않은데, G∘F ~= id_C가 있어 자연 동형이면
C와 D를 isomorphic처럼 볼 수 있게 됩니다.
지금부터는 거의 모두 상상입니다. 틀린 걸로 확인되면 모두 지울 예정입니다.
(너무 길어져, 이 부분만 따로 떼어 글을 올렸습니다. Adjunction에서 η와 ϵ의 화살표 방향이 반대인 이유)
자연 변환은 한 카테고리에서 다른 카테고리로 가는 펑터를 변환하는데, 이 때 변환한 값도 원래의 카테고리들을 벗어나지 않습니다. F∘G 합성의 정의역, 치역을 보면 id_D와 같은 D -> D로 원래 것과 같습니다. 사실은 D -> C -> D로 무려 현재 카테고리를 벗어났다가 돌아 오고 있지만, id_D와 같은 동작을 하게끔 하려는 게 목적입니다. 이 걸 척학적이라고 해야 할지, 인문적이라 해야 할지 모르지만, 그동안 “isomorphic하다” 라고 생각한 것들이, 시작과 끝을 제외하면 무슨 복잡한 일을 하고 있을 수도 있다는 생각이 듭니다. 컴퓨터의 computation과 달리 시간이란 양이 존재하지 않는 수학 세계에서는 얼마나 오래 걸리는 작업을 하든, 시작과 끝만 같다면 같은 것이니까요. 과정은 중요하지 않고, 결과만 같으면 같은 것입니다.
처음 Adjunction을 보고 떠올린 상상이, “달나라를 다녀와도 돌아 올 수만 있다면, 아무일도 일어나지 않은 걸로 해 줄게.” 입니다.
지금까지는 “같음”의 정도는 완전히 같음(이 건 수학적 정의를 모릅니다.) > 동형Isomorphic > 준동형Homomorphic 정도의 구분을 하고 있었는데, Homomorphic 중에 Adjunction이 있는 관계를 특징지을 수 있습니다.
우선, 여기선 같음의 기준을 Isomorphic으로 잡고 얘기를 이어가겠습니다.
F∘G 펑터 합성에서 id_D펑터로는 갈 수 있지만 돌아오지 못하는 자연 변환이 있고, G∘F 펑터 합성에서 id_C펑터로 갈 수 있는데, 돌아오지 못하는 자연 변환이 있는 경우를 생각해 보겠습니다. 돌아오지 못한다는 건, 무언가 처음의 정보를 잃어버렸다는 얘기입니다. 하지만, 잃어버린 정보가 그다지 필요한 정보가 아니었다면, 무시하고 같게 볼 수 있을 정도의 관계일 경우도 있습니다. 조금씩 틀어진 걸 보정하려면 언뜻 생각하기에 아래 자연 변환이 있으면 될 것처럼 보입니다.
ϵ': F∘G -> id_D
η': G∘F -> id_C 대부분의 텍스트에선 따로 설명없이 F∘G∘F, G∘F∘G가 등장하는데, 왜 이들이 조건에 등장하는지 말해주지 않고 시작하는 자료들이 많습니다. (Universal property로 접근하면 등장 이유가 좀 더 잘 보이긴 합니다.)
카테고리에선 대상이 뭔지 관심 없습니다. 두 카테고리가 isomorphic인지 본다면, 한 대상에서 출발해서 돌아온 대상이 같은 걸 보는 게 아니라, 둘 사이를 오갈 수 있는 펑터 F와 펑터 G가 있을 때, F의 경우 F로 갔다가, G로 돌아온 대상이 같은 가 보는 게 아니라, 돌아온 대상에 또 F를 적용했을 때, 동작이 변하지 않는 걸 보는 겁니다. 이 걸 식으로 표현하면 F에서 F∘G∘F로 갔다가 F로 돌아 올 수 있고, G에서 G∘F∘G로 갔다가 G로 돌아올 수 있냐를 보는 식으로 표현합니다. 그럼, 대상을 전혀 언급하지 않을 수 있습니다.
F∘G∘F = F
G∘F∘G = G아무 작업 없이 위 식이 성립하면 isomorphic입니다. 딱 isomorphic은 아니지만, 특정 작업으로 관계를 isomorphic과 비슷하게 만들면, 특정 조건하에선 isomorphic처럼 볼 수 있습니다. 과연 위에 두 자연 변환 ϵ',η'으로 가능한지 따라 가 보겠습니다.
별도로 정리한 글을 보시는 게, 좀 더 이해하기 편합니다. Adjunction에서 η와 ϵ의 화살표 방향이 반대인 이유
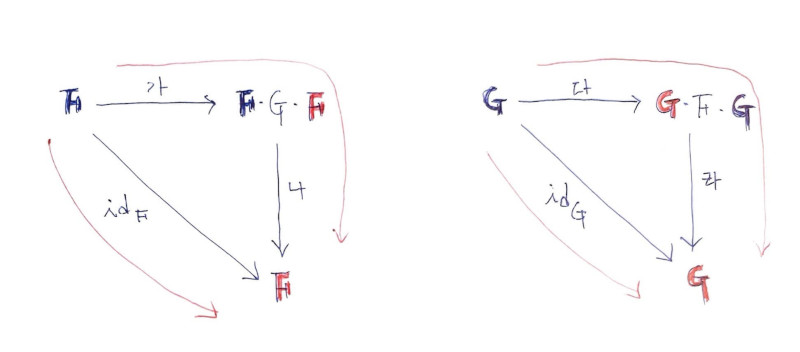
카테고리 이론은 다이아그램 체이싱을 하며 대체(가환)commute 경로를 찾는 작업이 기본이라 합니다. 대수에서 왼 쪽 = 오른 쪽 식과 같은 의미입니다. 빨간색 화살표들이 서로 commute하도록 만드는 게 목표입니다.
나∘가 = id_F 자연 변환
라∘다 = id_G 자연 변환F -> F∘G∘F 변환이 들어가야 하고,F∘G∘F -> F 변환이 들어가야 하고.G -> G∘F∘G 변환이 들어가야 하고,G∘F∘G -> G 변환이 들어가야 합니다.위 식이 성립하게 만들기 위해, 현재 가지고 있는 유일한 변환 ϵ', η'을 활용해 보겠습니다.
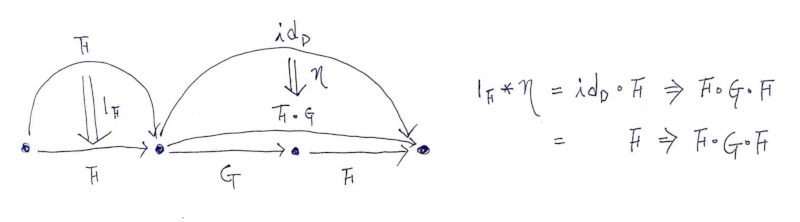
*은 자연 변환 수평 합성, 1F는 F에서, 1G는 G에서 항등 자연 변환을 뜻합니다.
1F * (id_C -> G∘F) 자연 변환이 들어가야 하는데, 우리 손엔 반대 모양 η': G∘F -> id_C만 있습니다. 실패(F∘G -> id_D) * 1F 자연 변환이 들어가야 하는데, 마침 ϵ': F∘G -> id_D가 딱 이 모양입니다. 성공(id_C -> G∘F) * 1G 자연 변환이 들어가야 하는데, 마찬가지로 우리 손엔 없습니다. 실패1G * (F∘G -> id_D) 자연 변환이 들어가야 하는데, 마침 ϵ': F∘G -> id_D가 딱 이 모양입니다. 성공※ 자연 변환 수평 합성Natural Transformation Horizontal Composition
F에서 항등 자연 변환 1_F를 그냥 F로 표기한 곳도 있습니다. 혹시 제가 모르는 표기 방법이나 내용이 있나 했는데, 맥락에 따라 알아서 해석해야 된다고 합니다. (@Ailrun님 감사합니다) 자연 변환 합성은 당연히 자연 변환끼리 합성하는 것입니다. 자연 변환 수평 합성의 결과는 자연 변환입니다. 아래 그림의 결과 자연 변환 F => F∘G∘F를 펑터 F에 적용하면 F∘G∘F를 얻습니다. (수평합성은 마치 튜플자리에 맞는 것끼리만 자연 변환을 적용하는 느낌입니다. 이 무슨 인포멀한 말이냐 하면, 자연변환 1F * η을 F∘id_C 합성 펑터에 적용하면, 1F는 F에, η는 id_C에 적용해서 최종 합성된 펑터 F∘G∘F를 얻습니다.)
왼 쪽 = 오른 쪽 둘을 같게 만들 때, 꼭 한 쪽만 변형할 필요는 없습니다. 아래처럼 놓고 다시 한 번 체이싱을 해보겠습니다.
ϵ'': id_D => F∘G
η'': id_C => G∘Fη''이 딱 맞고, 성공ϵ''은 반대입니다. 실패η''이 딱 맞고, 성공ϵ''은 반대입니다. 실패결국 Adjunction 텍스트에 나오는 서로 반대 방향의 자연 변환 ϵ'과 η''을 다음처럼 준비하면 다이아그램 체이싱에 성공할 수 있습니다.
ϵ: F∘G => id_D
η: id_C => G∘F위 그림을 보면 F∘G∘F에서 앞에 F와 뒤에 F의 색을 달리 했습니다. 제 눈엔 독특한 특징으로 보이는데 아직 속 뜻은 잘 못 찾고 있습니다. F와 같아지려면, 앞에 F가 살아남아도 되고(G∘F를 id_C로), 뒤에 F가 살아 남아도(F∘G를 id_D로) 되는 상황입니다. Adjunction이 가능한 이유가 여기에 있다고 상상하고 있습니다.
@todo 혹은 F∘G∘F에서 앞에 F와 뒤에 F를 반드시 처음의 F, 마지막 F와 연관지을 필요 없다고 본다면, 색깔은 무의미합니다. 아직 고민 중입니다.
이 번 글을 정리한 목적은 바로 이 특징 때문입니다. 속 뜻, 직관이 뭘까에 대한 상상입니다.
아래 @Ailrun님 답을 힌트로, 생각 저글링을 해봤습니다.독특한 특징1
F∘G를,G∘F를 연관짓는 툴(ϵ,η)은 가지고 있지만,F,G단독으로 연관 짓는 툴은 없습니다. 그런데, 마침 보고 있는 대상은F∘G∘F와G∘F∘G입니다. 우연일까요?톡특한 특징2
F∘G = id_D에 내포되어 있는 조건(정보)을 쪼개보면(분해)
(1) F∘G -> id_D 자연변환이 있다.
(2) id_D -> F∘G자연변환이 있다.
(3)둘이 합치면 처음으로 돌아가는 매핑이다.
G∘F = id_C도 마찬가지로
(4) G∘F -> id_C자연변환이 있다.
(5) id_C -> G∘F 자연변환이 있다.
(6)둘이 합치면 처음으로 돌아가는 매핑이다.그런데 여기 여섯 개 중
(1),(5)만 뽑아 위 삼각형 다이아그램 체이싱이 가능합니다. 동형이라면, 갈 때 썼던 펑터의 역펑터로 왔을텐데, 마치 올 때는 다른 집 역평터를 빌려서 돌아오고 있습니다. 우연일까요?id스런 동작을 못하는 F∘G 와 G∘F는 무슨 의미일까요?
여기 상상에 쓰인 아이디어는 우리가 하나라고 보고 있는 조건이 사실은, 여러 정보로 분해factorize할 수 있는 것일 수도 있다입니다.
(1)만 있고, (2)가 없다는 얘기는 (1) 동작을 하며 잃어버리거나 추가되는 정보가 있다는 얘기입니다. (4)도 마찬가지입니다. 두 번이나 정보 변형이 일어났는데, 처음과 같다고 보는 상황입니다.
Thu Nov 30 05:01:22 PM KST 2023 작성 중… @todo
다른 글에서, 모든 값을
id가 적용된 Computation으로 보자는 생각을 얘기했었는데, Adjunction도 비슷한 느낌으로 본다면,F펑터는id_D∘F∘id_C로 볼 수 있고,G펑터는id_C∘G∘id_D로 볼 수 있습니다.
모나드에서는 return이 번뜩이는 센스라 생각했는데, Adjunction에선 화살표 반대가 그런 듯 합니다.
과연, 화살표 반대 방향은 위처럼 쫓아가다 나온 것인지, 아니면 내포된 속 뜻이 있어, 단 번에 서로 반대 방향의 자연 변환을 준비해야 되는 걸 알았는지 지금은 모르겠습니다. 속 뜻에 대한 질문에 @Ailrun님으로부터 아래 같은 답을 받았습니다.
@Ailrun:
f∘g = id,g∘f = id가 가능하면,g의 정의역domain과 치역codomain이 같은 수준의 정보를 가지고 있습니다.
만약에 둘 다를 아래와 같이 정의하면ϵ: F∘G => id_D η: G∘F => id_C -- 원래 정의는 id_C => G∘F
F∘G나G∘F가id에 비해서 훨씬 “약한” 녀석이어도 (함수로 따지자면id_C나id_D라는 치역보다 훨씬 적은 정보만을 가지고 있어도) 얼마든지 두 자연 변환을 줄 수 있기에C와D의 강한 관계를 나타내는 대표자로서F와G를 쓰기 힘듭니다.
마찬가지로 반대로만 정의하면ϵ: id_D => F⋅G -- 원래 정의는 F∘G => id_D η: id_C => G⋅F
id_C에는 포함되지 않는 아무 온갖 쓸데없는 추가 정보를 포함하고 있어도, 문제가 없기 때문에 또 제약이 너무 약하다고 할 수 있습니다.
둘 중 하나 방향을 뒤집게 되면, 추가적인 제약이 들어있는 것과 같습니다. 위의 경우는 id_C, id_D 만큼의 정보(혹은 같은 양의 정보?)를 F와G의 합성도 가지고 있다는 얘기가 숨어 있다고 볼 수 있습니다.
결론은, 카테고리 C,D는 펑터F, G, 자연 변환ϵ, η가 있으면(Adjunction이 있으면) 같은 것처럼 볼 수 있을 정도로 같다(다르다)입니다.
※ ϵ은 counit이라 부르고, η는 unit이라 부릅니다.
정의만 읽어서 알 수 있는 공통점은, Adjunction, 모나드 둘 다 정보를 잃어버리면서도 같은 것이라 우기는 개념입니다. ϵ 과 η만 있다면, F와 F∘G∘F와 F∘G∘F∘G∘F,… 들을 모두 같은 척하고 볼 수 있습니다. 어딘가에서 모노이드와의 연관성이 나올 것으로 추측할 수 있습니다. (모나드는 M, M∘M, M∘M∘M,…들을 모두 같은 척하고 볼 수 있었습니다.)
참고. 프로그래머가 카테고리 이론 맛을 보려면, 바르토즈 밀레프스키 박사님을 피해갈 수 없습니다.
Adjunction - Bartoz Milewski
위 링크를 보면, 하스켈 의사 코드로 표현하고 있는데,
η_d :: d -> (R ∘ L) d
ϵ_c :: (L ∘ R) c -> c를 자연 변환이 잘 보이게 아래처럼 보고 읽었습니다.
η_d :: Id_D d -> (R ∘ L) d -- Id_D -> R∘L
ϵ_c :: (L ∘ R) c -> Id_C c -- L∘R -> Id_CR∘L을 m으로, L∘R을 w(m을 뒤집은)로 놓으면,
unit은 모나드의 return : a -> m a
counit은 코모나드의 extract : w a -> a
가 됩니다.
모든 adjoint 펑터 쌍은 모나드와 코모나드를 정의합니다. 모든 모나드와 코모나드는 adjoint 쌍으로 분해factorize할 수 있는데, 반드시 유니크한 하나의 쌍으로 나오지 않을 수 있습니다.
늘상 모나드를 쓰지만, Adjunction은 거의 쓰지 않는 이유가, adjoint 펑터 쌍으로 분해하면, Hask 카테고리를 벗어나는 무언가를 표현해야 할 때가 있어 안 쓰입니다. 하스켈에선 엔도펑터만 등장하는 Adjunction만 표현할 수 있습니다.
Adjunction으로 모나드를 표현할 수 있다는 말은, F, G, unit, counit을 적절히 섞어 return과 join (혹은 bind)를 만들 수 있다는 말입니다. 많이들 예시를 드는 State를 살펴 보겠습니다.
newtype State s a = State{runState :: s -> (a, s)}adjoint 펑터 두개를 찾아야 하는데, 굉장한 이론을 갖다 대기 전에 직관을 보겠습니다. State모나드가 하는 일은,
(가)상태 s를 받아서
-- 결과값 a와 같이 끌고 다니기 위해
(나)a와 s를 2튜플로 만듭니다.이렇게 직관적으로 두 단계로 나눌 수 있습니다. 코드로 쓰면 (가)s ->, (나) (, s)입니다. 더 변환이나 수정없이 바로 (가)가 Left adjoint G펑터고, (나)가 Right adjoint F펑터입니다. 웬일로 직관하고 조금도 빗나감 없이 딱 맞아 떨어집니다.
상상
모나드에서 모노이드의 이항연산을 두 단계로 쪼개 보던 거랑 연결됩니다. 모든 모나드가 아니라 하스켈의 모나드들은 (나)Right adjoint가한 카테고리에서 일어나는 펑터 합성인 Adjunction들로만 보면 될 것 같습니다.
State가 한 번 적용되어 있는 C와 State∘State가 적용되어 있는 D로 놓고,
C: s->(a,s)와 D: s->(s->(a,s),s) (runState와 람다는 생략)
G: a->(s->a), F: a ->(a,s), ※ 정보가 많은 쪽에서 적은 쪽으로 가는 걸 G로 둡니다
이제 정의를 따라가 보겠습니다.
(s->d) <----G----- d
| |
V V
c -----F----> (c,s)c를 (s->d)로 두면 (s->d) -> (s->d)=>d -> ((s->d), s)
unit은 id_C a => a -> ((s->a), s)
d를 (c,s)로 두면 (s->(c,s)) -> c=>(c,s) -> (c,s)
counit은 (s -> (a,s)) -> a => id_D a
return은 그냥 unit입니다.
bind는 (다)m과, m을 추가하는 함수를 받아, 적용한 뒤 (라)counit을 적용하면 됩니다.
(다) 작업을 실행한 후에는 s->(s->(a,s), s) 모양이고, 여기에 (라)를 적용하면,
s -> ( s -> (a,s) , s )
-- ^^^^^^^^^^
-- counit은 이 것만 꺼내고 다른 건 다 지우는 자연 변환입니다.s -> (a,s)만 남습니다. State펑터가 적용된 것에, State펑터를 한 번 더 적용후 counit을 쓰면 State펑터를 한 번만 적용한 것으로 돌아올 수 있습니다.
unit = return과 counit만 보이고, join은 안보였는데, “State펑터를 한 번 더 적용후 counit”이 바로 join입니다.
참고 - 바르토즈 박사님이 질문올린 쓰레드입니다. Monads as adjunction - stackoverflow
a -> b 모피즘을 보면 안되는 걸까? 보통 C카테고리에 있는 두 대상 a, b사이의 a -> b 사상이라 하면, 특정 사상 하나만을 뜻하는 것이 아니지 않나? a -> b만 해도 폴리모픽하게 정의한 모양일텐데, 이 것과 hom-sets 차이는? 준동형 사상 집합이란 뜻일텐데, 모피즘이 항상 준동형 사상은 아니지 않나? @todohom-sets의 자연 동형으로 Adjunctions을 정의할 수 있습니다. universal construction과 밀접하게 연결 됩니다. 여러 구성 절차construction로 분해factorize될 수 있는 고유한 사상이 있다는 말을 들으면, 어떤 집합과 hom-set간의 매핑이 있구나라고 생각하면 됩니다.?
자연 변환은 모피즘과 가환 다이어그램을 매핑합니다.
분명한 목적을 알려 주면 상상하는데 도움이 됩니다. 목표는 C와 D가 동형인가를 보기 위한 게 목표지만, 최종 목표 전에 중간 목표를 이렇게 잡을 수 있습니다. C에 있는 L d -> c 모피즘과 D에 있는 d -> R c 모피즘을 동형, 혹은 자연 동형으로 볼 수 있는가 입니다.
C에서 L d와 임의의 c를 잡으면, 그 둘 사이에 모피즘이 반드시 하나만 있는 게 아닙니다. 하나도 없을 수도, 여러 개일 수도 있습니다. 이 걸 hom-set C(L d, c)로 표현합니다. 이 hom-set의 도착지인 c를 R c로 D의 대상 중 하나와 매핑하면 아래같은 가환 다이아그램이 나옵니다.
@todo Hom-set으로 Adjucntion 정의하는 그림 추가
L, L d -> c, R로 가는 길과, d -> R c로 가는 길이 commute함이 보입니다. 이렇게, C(L d, c)와 D(d, R c) 사이에 isomorphism이 있으면 L, R로 Adjunction을 만들 수 있습니다.
카테고리 C에서 카테고리 Set으로 가는 펑터 (가), (나) 사이의 자연 변환과 (각 c마다, hom-set을 대상으로 갖고 있는 Set 카테고리의 hom-set 하나와 매핑한다고 볼 수 있으니, C -> Set 평터입니다.)
c -> C(L d, c) 펑터(가) -------- φ 자연변환 --------> c -> D(d, R c) 펑터(나)카테고리 D에서 카테고리 Set으로 가는 펑터 (다), (라) 사이의 자연 변환
d -> C(L d, c) 펑터(다) -------- Ψ 자연변환 --------> d -> D(d, R c) 펑터(라)φ와 Ψ가 서로의 역invertible이 된다고 합니다.
L, R 두 펑터 조합이 C, D에 있는 모피즘(여기선 hom-set)에 대해서 Id스런 일을 할 수 있게, 두 모피즘의 차이를 자연 변환으로 나타내려는 게 목적입니다.
Q. 자연 변환은 정의역과 치역이 같아야 하는데,
φ와Ψ는 도메인이 다르지 않나?
A. 도착지 hom-setC(L d, c),D(d, R c)는 카테고리Set의 대상이라 보고,C카테고리의 대상c와Set카테고리의의 대상을 매핑한 펑터 사이의 자연 변환은 결국Set카테고리의 모피즘입니다. 마찬가지로d와Set을 매핑하는 펑터 사이의 모피즘도Set카테고리의 모피즘입니다. 이 둘 모피즘 모두Set에 있으니 합성할 수 있습니다. 합성한 것이 isomorphism이 되면, 돌고 돌아왔지만C와D를 isomorphic처럼 볼 수 있게 됩니다.
카테고리가 같은가(얼마나 닮았나)를 보려면, 둘 사이를 오가는
펑터 조합이Id_C,Id_D와 같은 동형인지를 보고, 없다면,
펑터 조합과Id_C,Id_D사이의 자연 동형인가 봅니다. 없다면,
펑터 조합과Id_C,Id_D들을 같게 만들 수 있는 자연 변환이 있는가 봅니다.
지금 제 수준으로 보기엔, 카테고리 이론은 결국 자연 변환 놀음 같습니다.
※ c가 모두 출력 쪽에 있을 땐 covariant 펑터라 하고, d는 모두 입력 쪽에 있으니 contravariant 펑터라 합니다. 여기서 급하게 알아야 될 건 아닐 겁니다. 참고 - Covariant, Contravariant, Positive, Negative
hom-set을 이용한 정의를 쫓아가면 η: G∘F <- Id_C가 화살표가 당연하게 뒤집혀져 있어야 하는 게 보이긴 하나, 아직도 찜찜합니다. 처음, Adjunction 개념을 세운 학자는 왜 이런 생각을 했을까요? 첫 번째 방식의 정의를 쫓아가 보면, 화살표가 뒤집힌 것만 나오는 게 아닙니다. 여러가지 조합이 가능한데, 왜 하필 그 중 Adjunction 인 것에만 이름을 붙였을까요?
글이 길어져 별도의 글로 올렸습니다. Adjunction에서 η와 ϵ의 화살표 방향이 반대인 이유
C, D 둘이 얼마나 같은데?
C, D 둘은 다르지만, isomorphism으로 같게isomorphic 볼 수 있는 것
※ “그 시스템에서 F는 upto isomorphism으로 유니크해” 이렇게 한글인 척 하는 영어 문장들을 가끔 만납니다. 시스템에 조금씩 다른 F, F', F'',… 들이 존재하지만, 이들을 isomorphic하게 볼 수 있는 isomorphism이 있으면, 결국 이들은 다 같은isomorphic 걸로 보고, 하나만unique 있는 것처럼 볼 수 있다는 말입니다.C, D 둘은 다르고, isomorphism도 없지만, 둘 간의 펑터 F, G 합성을 G∘F는 Id_C펑터와, F∘G는 Id_D펑터와 같게 볼 수 있게 하는 Natural isomorphism이 있는 관계야C, D 둘은 다르고, isomorphism도 없고, Natural isomorphism인 펑터 합성도 없지만, 펑터 합성을 Natural isomorphism과 비슷하게(같게) 볼 방법(변환 방법)이 존재하는 Adjunction이 있는 관계야.둘이 얼마나 같은지, 얼마나 밀접한 관계인지를 표현할 수 있는 Adjunction이란 툴이 하나 더 생겼습니다.
※ 아래는 과연 현실에서 동형과 달리 자연 동형이 어떤 직관으로 나타날까 고민하다 나온 상상입니다. 아래는 G∘F만 보겠습니다.
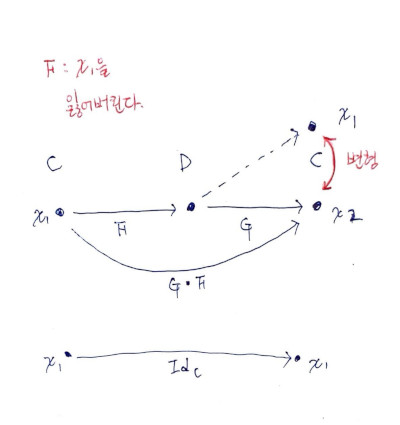
동형, 자연동형, Adjunction이 있는 관계는 그림에서 빨간 변형에 따라 구분이 되는 것으로 상상하고 있습니다. (동일한 일이 F∘G에도 일어납니다.)
Id_C나 Id_D에서 역으로 F∘G나 G∘F를 찾을 수도 있어야 하니 얼마나 변형됐는지 정보를 잃어버리면 안됩니다.※ 변형이 일어났다는 말은, 곧 F가 x1이란 정보를 잃어버리면서 온다는 얘기로 보입니다.
ϵ과 η는 id들과 일대일 대응이 아닙니다. 무언가 정보를 잃어버리면서 Id와 비슷한 일을 합니다. 모나드와 마찬가지로 쓸모 없는 정보를 잃어버리거나 합치면서 같은 모양이 가능한 것들이 있다면, Adjunction으로 모델링을 시도해 볼 수 있습니다.
아마도 이런 인포멀한 접근이, 전공 선수분들한테는 의미가 없을지도 모르겠습니다. 전 현실 문제를 보고, 펑터로 이리 저리 변환을 하는데, 어떤 경우가 보이면 Adjunction을 이용해 모델링해야겠다란 생각이 들 수 있도록 하는 게 목표입니다.
참고. 다음 글은 찾은 자료 중, 직관에 대한 설명이 가장 많이 등장하는, 제 입맛에 딱 맞는 글입니다. 예시를 벡터 스페이스로 들고 있어 그리 쉽지는 않지만, 딱딱한 정규 텍스트들보다는 좋았습니다.
What is an Adjunction? Part 1 (Motivation) - math3ma
What is an Adjunction? Part 2 (Definition) - math3ma
참고. 하스켈 코드로 Adjunction 보기
From Adjunctions to Monads - Stephen Diehl
Adjunctions And Battleship
Mon Nov 27 03:45:47 PM KST 2023 작성 중