Adjunction에서 η와 ϵ의 화살표 방향이 반대인 이유

Adjunction을 만드는 두 Adjoint 펑터로 모나드 표현하기 글을 올리다가 너무 길어 따로 떼어냈습니다. 역시나 수학도들을 위한 formal한 설명은 아닙니다. 하스켈 프로그래머는 이 정도만 알아도 충분하다 하는 정도의 informal한 내용입니다.

Adjunction 공부를 하면서 hom-set을 이용한 정의를 보다 보면, ϵ: F∘G -> Id_D와 η: G∘F <- Id_C가 서로 반대 방향인 이유가 별로 궁금하지 않을 수도 있습니다. 그냥 자연스러워 보여서 딱히 텍스트들도 짚고 넘어가지 않는 경우도 많습니다. 하지만, 바닥부터 스스로 만들어 보면 어떤 생각들이 나올까 따라가다 보면, 방향이 반대인 것에서 막힙니다. 전 여기에 Adjunction의 비밀이 있다고 보고 캐 봤습니다.

F펑터로로 C에서 D로 갔다가, G펑터로 D에서 C로 돌아왔는데, 원래 출발지로 돌아왔다면, 또 F펑터로 C에 가도, 처음 F펑터로 간 것과 다르지 않습니다. D에서부터 시작해서도 같은 동작이 확인되면, “아, F와 G만 있으면 둘이 isomorphic하게 볼 수 있겠다”할 수 있습니다.

F <--------isomorphic--------> F∘G∘F
G <--------isomorphic--------> G∘F∘G
이렇게 일직선으로 주욱 가면 고민할게 없지만,

틀어짐을 보정할 수 있다

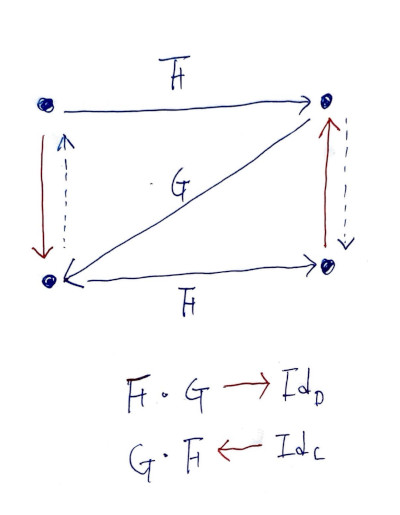
F와 G의 합성이 isomorphism 역할을 못한다면, 일직선 모양이 아니라 지그 재그 Z 모양입니다. unit,counit으로 정의를 하다보면, F∘G로 틀어진 걸 Id_D로 보고, G∘F로 틀어진 걸 Id_C로 보려고 필요한 자연변환이, 꼭 ϵ, η 조합이 아니더라도 가능할 것처럼 보입니다.

ϵ: F∘G -> Id_D
 : G∘F -> Id_C

 : F∘G <- Id_D
η: G∘F <- Id_C

ϵ: F∘G -> Id_D
 : F∘G <- Id_D

 : G∘F <- Id_D
η: G∘F <- Id_C

왜 특별히 ϵ, η를 고르고 F, G와 합쳐 멋지게 Adjunction이란 이름도 붙여줬을까 궁금해졌습니다. 어떤 텍스트에선 서로 inverse하게 만들어 중간에 F나 G를 끼워¹ 넣어 합성하기 위한 것이다로 설명하고 넘어가기도 합니다. 하지만, 이 설명만으론 찜찜했습니다.

결론부터 말하면 ϵ, η 조합이 가장 의미가 있습니다.

다른 조합도 틀어짐을 보정할 수 있긴한데, 제약이 너무 약해 특별한 뭔가로 취급하기엔 무리가 있습니다.

지금부터 좇아가 보겠습니다.

동형Isomorphic

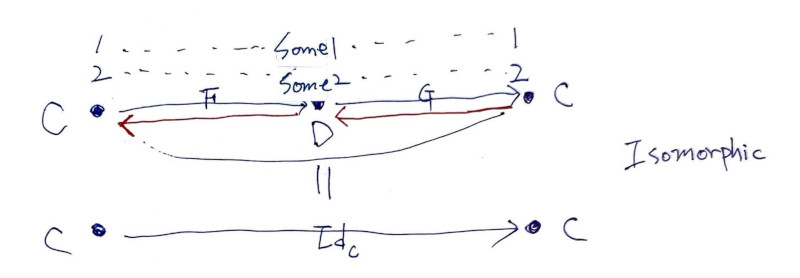
각 C = {1,2}, D = {Some1, Some2} 원소를 가지고 있어, 이들을 위 그림처럼 매핑하면, C와 D는 동형Isomorphic입니다.

이제 Isomorphic이 아닌 친구 중 가장 익숙한 Maybe 펑터로 살펴 보겠습니다.

※ 이하 그림에선 Int를 1,2까지만 표기했습니다.

의미 있는 관계를 만들지 못한다

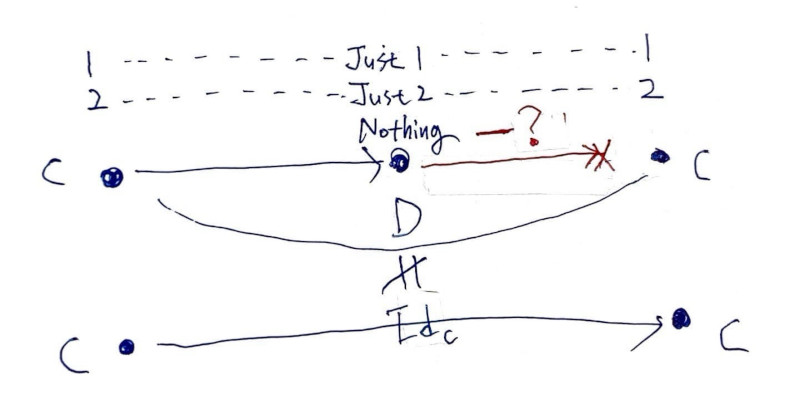
Nothing이 갈 곳이 없어 이렇게는 동형 비슷한 걸 만들 수가 없습니다.

자연 동형Natural Isomorphic

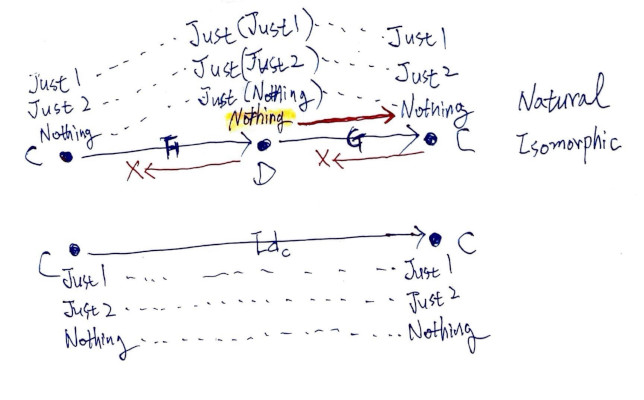
C:Int와 D:Maybe Int가 아닌, C:Maybe Int와 D:Maybe (Maybe Int)를 대상으로 두면 Just (Nothing)을 Nothing으로 우겨 넣으며 동형 비슷하다고 우길 수 있습니다. 참고 - 모나드, 같음 - m (m a)와 m a는 얼마나 다를까?

G∘F는 Id_C와 동일한 동작을 합니다. 자연 동형입니다. Just 1에서 출발해서 Just 1로, …, Nothing에서 출발해서 Nothing으로 돌아올 수 있습니다. C와 D는 동형Isomorphic은 아니지만, 둘 사이를 오가는 펑터 F, G 합성 중 G∘F는 Id_C와 자연 동형Natural Isomorphic입니다. 그냥 동형일 때보단, 뭔 짓을 해야하긴 하지만, 그래도 이정도면 많이 닮았으니 같은 걸로 볼 수 있을 것만 같습니다. G∘F를 봤으니, F∘G도 살펴 봐야 합니다.

※ 사실 자연 동형이 안되는 걸 찾으려 했는데, Maybe와 Maybe∘Maybe사이의 G∘F는 Id_C가 자연 동형입니다. @todo 아마도 Free Functor를 이해가 필요하다.

자연 변환Natural Transformation

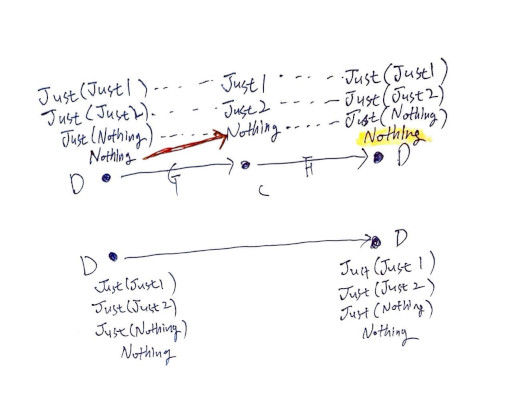
Nothing으로 출발해서 Nothing으로 돌아온다는 보장이 없습니다. C로 가면서 구조의 일부를 잃어버렸기 때문입니다. Id_D와 다른 동작을 하니 자연 동형이 아닙니다.

이제, 이 상황에서 Id_D와 동형은 아니지만, F∘G <- Id_D 또는 F∘G -> Id_D 자연변환을 정의하려 합니다.

펑터 합성이 된다는 건, 서로의 정의역 공역이 일치해야 합니다. (아래를 작성하며, 공역codomain과 치역range 중 어느 것으로 설명해야 하는지 혼동이 있습니다. 전사surjective라면 뭐든 상관없으니 뭘 써도 되겠지만요. F와 G의 정의는 별 개입니다. F의 공역과 치역이 다를 때(D의 모든 구성원들이 C와 매핑되는 건 아닐 때), G의 정의역은 F의 치역과는 다릅니다.)

F도 Id_C도 둘 다 C에 있는 펑터로 정의역은 같습니다. F의 공역은 G의 정의역(D)과 같고, Id_C의 공역은 C입니다.
G도 Id_D도 둘 다 D에 있는 펑터로 정의역은 같습니다. G의 공역은 F의 정의역(C)과 같고, Id_D의 공역은 D입니다.

C보다 D가 훨씬 더 큰 구조로, 둘이 완전히 다르게 생긴 걸 상상해 봅시다. G∘F에 있는 훨씬 많은 정보들이 있어도 Id_C 매핑은 가능합니다. 아래 그림에서 C와 D가 만나는 뾰족한 부분이 아무리 커도 전사로 모두 Id_C와 매핑하는 G∘F -> Id_C를 얼마든지 만들 수 있습니다. 너무 제약이 없어 특별할 게 없습니다. 하지만 반대로 두면 Id_C가 가진 정보만큼만 G∘F와 매핑합니다. F의 정의역과 G의 공역은 Id_C와 같다는 말입니다. 마치 F공역과, G의 정의역의 최소를 Id_C로 제한하는 것과 같습니다.

F∘G는 움푹 들어간 부분이 아무리 올라와도 Id_D보다는 커지지 못하는, F의 정의역과 G의 공역의 최대 크기를 Id_D로 제한 하는 것과 같습니다.

※ 대상 수가 많고, 모피즘이 많은 걸 큰 구조라고 부르겠습니다.

말로 쓰니 매우 복잡합니다.

Maybe (Maybe Int) 구조는 Maybe Int의 구조(Just _, Nothing)와 동일한 구조(Just (Just _), Just (Nothing))는 그대로 보존하고 있고, 추가로 Nothing이란 구조를 가진 더 큰 도메인을 가지고 있습니다. 이 걸 도형의 크기로 구분해서 그렸습니다. 아래 그림에서 C를 Maybe Int로, D를 Maybe(Maybe Int)로 보면 됩니다.

F: C -> D는 작은 구조 Maybe Int에서 큰 구조 Maybe(Maybe Int)로 가고 있습니다.
G: D -> C는 큰 구조에서 작은 구조로 가고 있습니다.
Id_C: C -> C는 작은 구조에서 작은 구조로 가고 있습니다.
Id_D: D -> D는 큰 구조에서 큰 구조로 가고 있습니다.

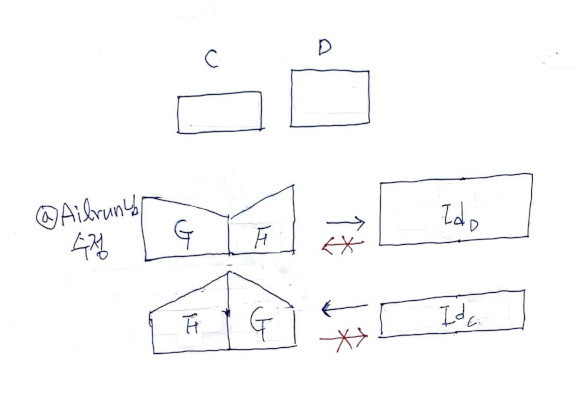
위에 말로 쓴 매우 복작한 걸 한번에 표현할 그럴싸한 그림이 떠올랐습니다.
펑터를 표현하는 상자는 왼 쪽면이 입력, 오른 쪽 면이 출력으로 두겠습니다.

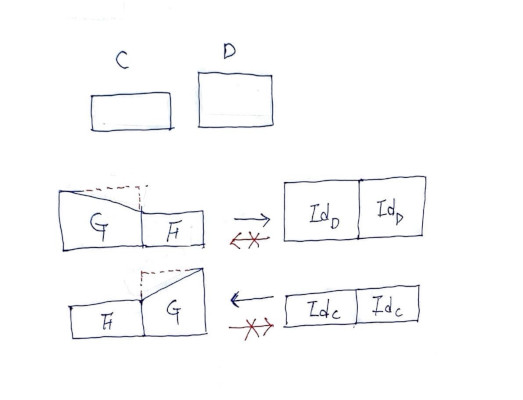
※ Id 상자들을 둘로 나눠서 본 이유는 수평 합성을 따져 보려고 한 건데, F, G 각 각 독립적으론 Id_D, Id_C와 정의역, 공역이 달라 의미가 없습니다. 아래 그림처럼 그냥 하나로 보는게 더 잘 들어 맞습니다.

화살표 입력에 있는 도형은 출력에 있는 도형에 반드시 들어 갈 수 있어야 합니다. 위에 X표를 해둔 빨간색 화살표로 바꾼다면 도형들을 그대로 넣을 수 없는 상황입니다. 자연 동형이 아니라서 Id_C, Id_D로 만들 적당한 자연 변환을 준비한다 해도, 아무 조합이 되는 게 아니라, 지켜야 하는 제약이 있습니다. 적어도 G∘F합성은 Id_D를 넘지 않는 정보를 가져야 하며, F∘G 합성은 Id_C보다는 큰 정보를 가지고 있어야 합니다.

(최종 입출력 메타포가 잘 보이도록 @Ailrun님이 아래와 같이 F, G의 도형 모양을 바로 잡아 주셨습니다. 감사합니다.)

정보량을 도형의 크기로 나타낸 것으로, 입력에 있는 F∘G 도형은 Id_D 도형에 들어갈 수 있으며, G∘F는 반대로 Id_C가 G∘F에 들어갈 수 있습니다. 하지만, 각 각 화살표를 뒤집으면 안에 넣을 수 없음을 알 수 있습니다. 어디서 옮겨온 그림이 아니라, 각 각의 정의역 공역들이 얽혀 있어, 한 번에 표현하기 위해 직접 상상한 그림입니다.

그림 해석을 요약하면
F∘G 가운데가 아무리 올라와도 Id_D보다는 작을 것이며,
G∘F 가운데가 아무리 내려가도 Id_C보다는 클 것이다입니다.

뾰족 튀어 나온 부분이 내려갈수록, 움푹 들어간 곳이 올라올 수록 C와 D는 점점 닮아갑니다.
만일, Isomorphic한 상태라면, C,D,F∘G, Id_D, G∘F, Id_C는 모두 같은 크기의 도형이 됩니다.

아주 인포멀하게 말하면, 둘이 다른 모양인데 연결하려면, 그 사이에 Adjunction을 두는데
Id_C가 가진 정보량 =< F와 G가 가진 정보량 =< Id_D가 가진 정보량
정도가 가장 쓸모있는 의미를 가진다는 겁니다. 그림에서 Adjunction을 Id_D보다 훨씬 크게 그려 놓고, 보정해주는 자연 변환을 정의할 수도 있고, Id_C보다 훨씬 작게 그려 놓고, 자연 변환을 정의할 수도 있습니다. 하지만, 그렇게 정의하는 건 (아마도 거의) 모든 것에 적용할 수 있는 것이니, 특별한 의미가 없습니다. Adjunction의 정보는 Id_C보다는 크고, Id_D보다는 작아야 의미가 있다고 보는 겁니다.

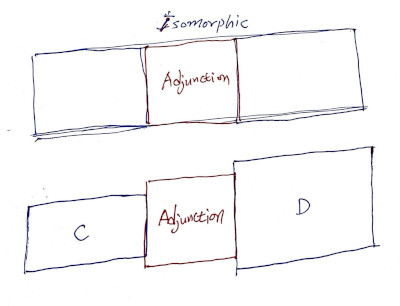
왜 이름이 Adjunction인지 보여주는 그림이라 생각합니다. 연결junction을 도와주는ad 것!
Adjunction은 C보다는 크고, D보다는 작아야 합니다.

카테고리의 Isomorphism은 C, D, Adjunction의 크기가 모두 같은, 즉 Adjunction의 한 사례입니다. 이 경우, 자연 변환은 Id로 존재한다고 보면, 모든 Isomorphic 관계에도 Adjunction은 존재합니다. 둘이 같은지를 볼 때(둘이 연결을 할 때로 비유)는 항상 Adjunction이 필요합니다.

Adjunction이 뭘 의미하는지 보기 위해, 직접 상상한 그림이니, 혹 오류가 있다면 꼭 댓글이나 e메일 부탁드립니다.

2024.1.14

결론

두 카테고리 중 하나가 가진 구조를 다른 쪽이 완전히 보존하며 추가적인 구조를 가진 상황이라면, 정보가 불균형하여 Isomorphism이 있을 수 없어 Isomorphic으로 볼 수 없는 상황입니다. 하지만 큰 구조에서 작은 구조로 올 때 틀어짐을 감수할만한 상황이라서, 위 타입의 자연변환 두 개만 정의할 수 있다면, 적당히 같다고 우겨 볼 수 있습니다.

(마치, “같다”는 하나의 조건을 여러 개로 쪼개어factorize, 둘이 스페셜한 관계라고 할 수 있는 최소한의 제약을 추린게 ϵ, η까지는 남겨 둔다 느낌입니다. 혹 더 깊이 들어가서 조건을 더 여러 개로 쪼개면, 덜 닮았지만 의미 있는 경우가 또 나오는 게 아닐까요? )

어디선가 글을 읽다가 두 구조에 “Adjunction을 줄 수 있다”, “Adjunction을 정의할 수 있다”라고 한다면, “두 구조간의 불균형 정보를 수긍이 가는선에서 무시한다면 같게 볼 수 있는 방법이 존재한다”라고 받아들이면 됩니다.

둘은 Adjunction 관계야가 아니라, Adjunction을 가질 수 있는 관계, 혹은 Adjunction이 있는 관계야 라고 말하는 게 맞겠습니다.

프로그래밍에서 틀어짐이 꼭 중요하지 않은 예시로는, 지금 아는 건 모나드 밖에 없습니다. 모나드는 F, G가 엔도펑터인 Adjunction의 한 사례입니다.

• Writer모나드: "log1","log2"를 차례로 생겼지만, 최종 "log1log2"만 필요하다면, "log1"+"log2"해서 "log1log2"인지, 한 번에 "log1log2"인지 알 필요가 없다.
  
• Maybe모나드: Just(Nothing)이어서 Nothing인지, Nothing이어서 Nothing인지 알 필요 없다.
• Reader모나드: 환경값을 한 번 읽어 오든, 두 번 읽어 오든 달라질 게 없다.
• 1+2, 0+3, 2+1,… 뭐든 상관 없이 3만 알면된다. …

왜 화살표가 뒤집어져 있는지 어느 정도 이해는 가지만, 여전히 처음 정의한 수학자는 어떻게 이런 개념을 떠올렸을지 궁금하긴 합니다.

※ Identity란 뭘까요?
다른 것과 구별해서 특정지을 수 있는 뭔가 Identity라고 합니다. 다른 것들이 있다면 다른 것들과의 관계로 대상을 특정 짓는 홈펑터등으로 대상을 가리키기도 하는데, 혼자만 있다면 대상을 특정 짓는 것은 뭘까요? 카테고리 Cat에서 대상이 카테고리 C{a,b,c,모피즘들} 이라면 Id_C 펑터는 {a->a, b->b, c->c, 모피즘들의 id}을 뜻합니다. C라는 표현보다는 Id_C가 더 구체적으로 표현하고 있다는 생각이 듭니다. 카테고리 세계에서 대상은 아무런 성질이 없는 점입니다. 카테고리 C보다는 Id_C펑터를 가지고 훑어 보는 일이 더 많습니다.

※ 항상 Adjunction이 있는 걸로 보기
원래부터 같은 걸 보는 건 C->D로 가는 것, D->C로 가는 것 모두 보아야 합니다. Id_C도 마찬가지 입니다. Id_C를 Adjunction으로 보면 Adjoint 펑터는 F = Id_C:C->C, G = Id_C:C->C 두 펑터와 ϵ=id, η=id로 볼 수 있습니다.

Adjoint 펑터 F,G, 그리고 η를 써서 C에서 C로 아올 수 있고,
Adjoint 펑터 F,G, 그리고 ϵ를 써서 D에서 D로 돌아올 수 있다면,
동형은 아니지만, 그래도 특별한 사이로 보는 겁니다.