※ 블로그 글의 편집 결과가 그런대로 볼만하게 나오는 게 오히려 문제입니다. 꼭, 정확한 지식인양 보일 수가 있거든요. (조금이라도 검증을 통과하면 그림들을 다시 그리겠습니다. 지금은 허술한 그림이 오히려 목적에 맞습니다.) 아래 글은 정확한 내용이라 검증되지 않았습니다. 다른 텍스트를 보고 아직 이해가 안간, 주로 프로그래머 분들과, 뭐가 맞는지 상의하기 위해 올리는 글입니다. 심오한 수학적 정의를 원하는 분한테는 어울리지 않는 곳입니다.
A,B,C(순서는 형부터)가 있을 때,A보다는 작고”, “(나) C보다는 크다”B뿐이 없습니다. (가), (나) 모피즘을 이용해 B를 정의했습니다. (B를 특정지을 수 있습니다.)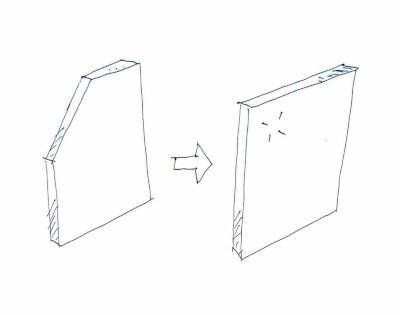
위 모피즘 그림의 사각형을 완성시킬 무엇은? . 삼각형 모양을 잘라 낸 어떤 도형으로도 삼각형을 가리킬 수 있습니다.
(A->B)를 (C->B)로 매핑한다.(A->B)를 (C->B)로 변환한다.(A->B)와 (C->B)의 차이를 나타낸다.A를 C로 바꾸는 A->C만 있으면 구현할 수 있을 것만 같습니다. ((A->C)->B) 이렇게요. 하지만 A->B는 블랙 박스입니다. 안에서 무슨 일이 일어나고 있을지 알 수 없습니다. A->Z->Y->X....C->B 이러고 있을지도 모르는데, 어디를 어떻게 손 댈지 알 수 없습니다. A->블랙 박스->B가 고차 함수가 아니고선, 블랙 박스에 들어가는 인터페이스 A와 붙이든지, 나오는 인터페이스 B와 붙이든지 해야 합니다. (※ 고차 함수를 받을 인터페이스도 결국 하나의 타입으로 표현되니, “항상”이라 해도 되겠습니다.)카테고리 이론에서 보면, (A->B) 자체를 대상으로 삼으면, 대상이 뭔지는 보지 않습니다. 그저 모피즘의 시작과 끝만 표시하는 점입니다. (A->B)가 가진 어떤 속성도 고려하지 않습니다.
일단, hom-set부터 보고 가겠습니다. hom(a,b)는 a에서 b로 가는 모든 모피즘의 집합이라고 합니다.
상상
Q. 그런데,a -> b라고 표현하는 것도 어차피a,b가 폴리모픽 아닌가요?a -> b라고 표현해도 같은 의미인 것 같은데, 왜 또 표현을 만들었을까요?
A.a -> b가 모피즘으로 쓰이지 않고, 카테고리에서 대상object 역할을 할 때,a -> b라고 쓰면,a -> b에서c -> d로 가는 모피즘b -> c와 혼란스럽게 섞입니다. 이 때hom(a,b) ---- b -> c ----> hom(c,d)로 표현하면 혼란을 줄일 수 있어서 만들어내지 않았을까 추측합니다.
Hom-Set은 준동형Homomorphism 사상 집합이란 이름인데, Hom-Functor는 뭘까요?
카테고리C를, 카테고리 C에 있는 모피즘들의 집합을 대상으로 가진 카테고리 Set로 매핑하는 펑터를 의미합니다.
상상
펑터 자체도 카테고리 구조를 보존하는 homomorphism이니, Hom을 붙이는 게 어색하지 않습니다.
Q. 그럼 hom-set처럼 펑터의 집합을 의미할까요?
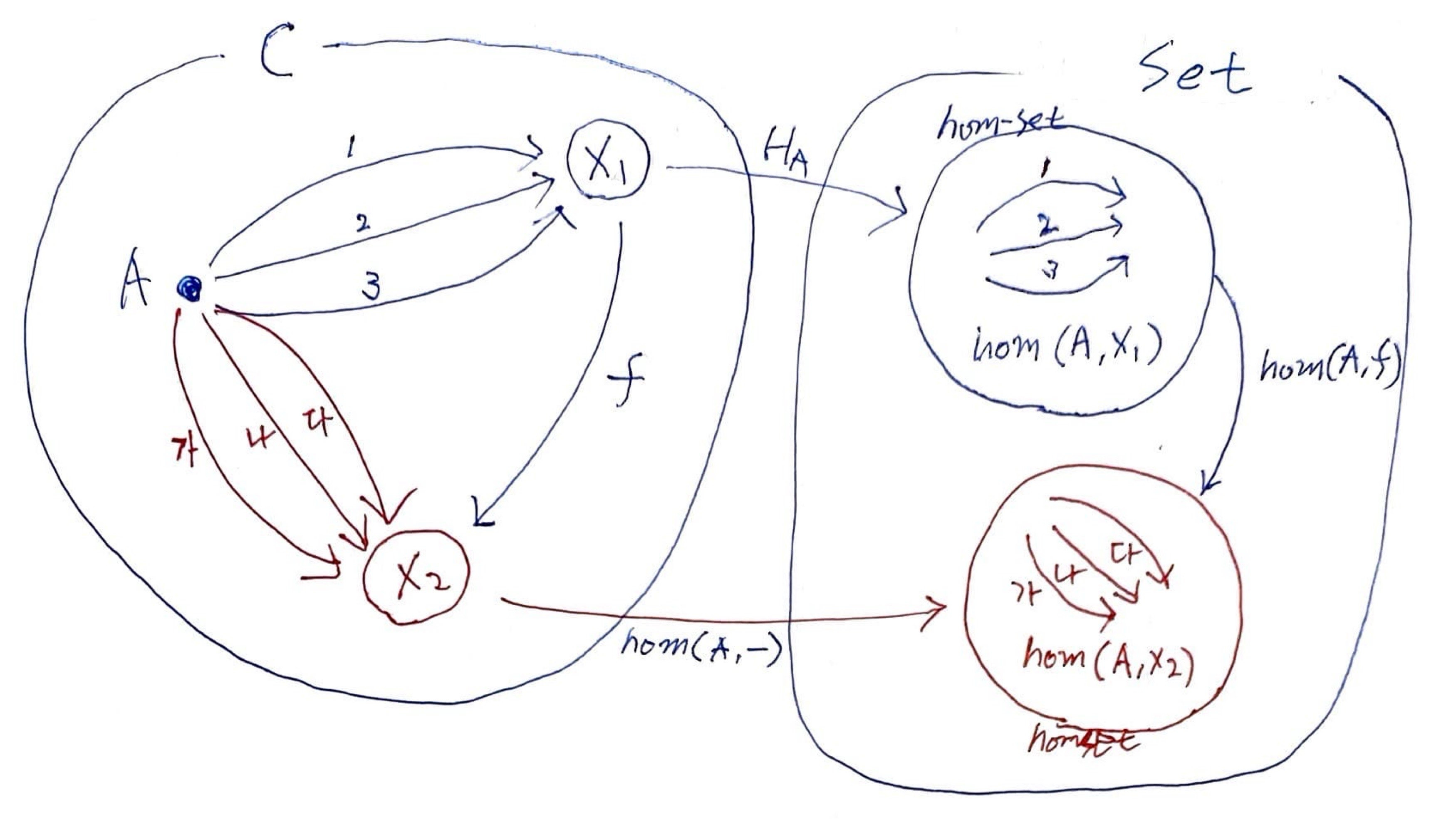
A. 처음Hom(A, -)를 봤을 때는, 이 자체가 구현처럼 보였습니다.X1 -> Hom(A,X1)이렇게 매핑하니까요.A는 카테고리C에 있는 오브젝트X1,X2, … 중 하나를 뽑아 홈펑터를 만듭니다. 그런데,A는 모든 오브젝트라 하니, 각각의 오브젝트에 대해 홈펑터Hom(X1, -), 홈펑터Hom(X2, -), …를 의미합니다.A를 폴리모픽하게 두어 폴리모픽하게 홈펑터를 표현합니다. (검증 필요)※ 정규 과정에 쓰이는 텍스트를 차분히 보지, 왜 상상해서 이런 말을 올리냐 할 수 있습니다. (다 보진 못하고, 2~3권 딱 해당 챕터의 도입부 정도만 보긴 했지만) 사람들이 이런 걸 별로 궁금해 하지 않는지, 짚어 주고 시작하는 텍스트를 못 찾았습니다. 그래서, 이런 상상 꼬리표가 달린 글들을 올립니다. 이런 글을 보고, 틀린 걸 발견하거나 다른 의견이 있으신 분들을 만나 이러쿵 저러쿵 하고 싶어 글을 올립니다만, 3년 넘게 운영하는 동안 의견을 주고 받을 분을 만나기가 쉽지 않네요.
보통 소문자 hom은 hom-set으로 쓰이고, 대문자 Hom은 hom-functor로 구별해서 쓰나 했는데, 딱히 대소문자로 가리진 않고, 위 링크 위키 텍스트에서 Hom(-,-), Hom(A,-)처럼 -가 들어가 있으면 hom-functor, -가 없이 Hom(A,B)면 hom-set을 가리키는 걸로 보입니다.
C에 있는 모든 대상 A, B들에 대해 Set으로 보내는 두 펑터를 아래와 같이 정의합니다.
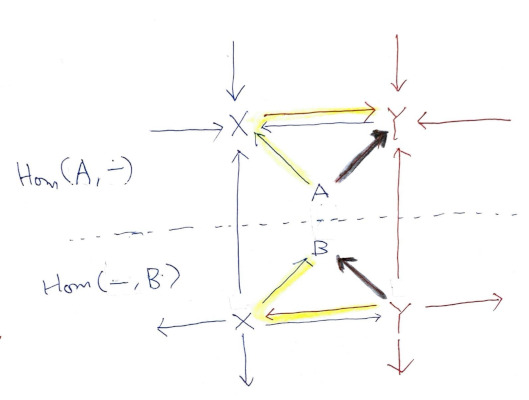
Hom(A, -)는 마치 하스켈 타입 생성자 같기도 하고, 함수를 인자로 받아, 가지고 있는 함수를 변형하는 고차 함수 같기도 합니다. 쓰고나서 보니, 펑터 인스턴스가 있는 타입 생성자와 fmap, 즉 펑터입니다.
Hom(A, -)에서, 설명을 위해 A는 일단 고정한 채로
아래와 같이 카테고리C에 있는 X,Y,... 대상을 Set카테고리의 대상 hom-Set에 매핑합니다.
X —> Hom(A,X) : A를 주면 X가 되는 함수
Y —> Hom(A,Y) : A를 주면 Y가 되는 함수
…
Hom펑터는 펑터니까 모피즘도 매핑해야 합니다.
f:X -> Y —> Hom(A,f): Hom(A,X) -> Hom(A,Y)
그런데, 여기 눈여겨 봐야할 성질이 하나 숨어 있습니다. 하스켈에서 펑터는
f를 변형한다고 보기도 하고, (a -> b) -> (f a -> f b)f를 적용한다고 해석하기도 합니다. (a -> b) -> f a -> f b주의: 함수 안에 들어 있는 걸 바꾸는 건 다른 문제입니다. 한참 헤맸는데,
Maybe x일 때fmap으로x에 함수를 적용할 순 있어도, 생각 스트레칭에서 말했듯이,Maybe (x -> y)에선 함수를 깨버리고 들어갈 수가 없습니다.x와y는 보이지 않습니다.(x -> y)자체가 대상object입니다. 대상을 변형할 수는 없고, 전에 합성을 하든, 후에 합성을 하는 수 밖에 없습니다. 안에 있는x에f를 적용한다는 메타포로 보면,Maybe안에 있는(x -> y)에f를 적용할 순 있어도, 더 들어가x에 적용할 순 없습니다.
※ 함수 펑터가 가지고 있는fmap을 쓴다면(->) a b에서a에 접근할 수 있습니다. 여기선Maybe의fmap으론 함수 펑터 안에 있는 대상에 도달하지 못한다는 말입니다.
A->X를 변환해서 A->Y가 되게 하려면, A->X 다음에 f: X->Y를 합성((X->Y) ∘ (A->X))하면 됩니다. 또는 새로운 구조 A->X 안 쪽에 있는 X에 f를 적용하는 것이 아니라, A->X의 결과로 함수를 빠져나올 X에 f를 적용합니다.
하나의 hom-Set Hom(A,X)에 들어 있는 모피즘(:A->X)을 g1, g2, ... 라 하면, Hom-Functor Hom(A,-)는 이 모피즘들을 각 각 f:(X->Y) ∘와 합성합니다. 결국 hom-set Hom(A,Y)에 있는 모피즘(:A->Y) f∘g1, f∘g2, ...로 매핑하는 모양이 됩니다.
g1 ----> f∘g1
g2 ----> f∘g2
...※ 모피즘 매핑을 보면 X -> Y에 펑터를 적용한 결과가 X -> Y 그대로여서 Covariant 펑터라 합니다.
(※ 보통 카테고리 이론에서는 대상을 구조가 없는, 아무 성질도 없는 점 쯤으로 생각합니다. 그런데, 만일 Hom(A,-) 펑터를 적용하니, 위와 같은 합성 성질이 나왔다면, 대상이 A->X를 가지고 있다고 유추할 수 있을 것 같습니다. (검증 필요))
※ Hom (A,-)는 컴퓨테이션을 거친 결과가 A는 아니라서, 전 Contravariant한 Hom (-,B)가 더 생각하기에 편한 듯 합니다.
B는 일단 고정한 채로
Hom(-,B)는 아래와 같이 매핑하는 펑터입니다.
X —> Hom(X,B) : X를 주면 B가 되는 함수
Y —> Hom(Y,B) : Y를 주면 주면 B가 되는 함수
…
모피즘 매핑을 보겠습니다.
(1) h:X -> Y —> Hom(h,B): Hom(X,B) -> Hom(Y,B) -- ???
(2) h:X -> Y —> Hom(h,B): Hom(Y,B) -> Hom(X,B)
(1)처럼 Covariant하게 정의하면 될 것 같은데, (2)로 Contravariant하게 정의하고 있습니다. 왜 이렇게 정의했을까요? (1)이 뭐가 문제인지 보기 위해, (1)로 정의해 보겠습니다. X->B 모피즘을 Y->B로 변환하려 합니다. 어떤 변환 과정을 거치든 시작이 Y이고 끝이 B입니다. X->Y와 X->B만 가지고선 시작에 Y를 둘 방법이 없습니다. 끝에 B를 둘 수 있는 X->B는 있으니, ∘ (Y->X)가 있으면 딱입니다. h^op:Y->X가 필요합니다. (h:X->Y에서 화살표가 뒤집어졌다고 ^opposite를 붙입니다.) X->B모피즘을 g1, g2, …라 하면, g1∘h^op, g2∘h^op, …와 매핑합니다. 결국, 함수의 입력 쪽에 X가 있다면 Contravariant한 정의만 가능합니다.
g1 ----> g1∘h^op
g2 ----> g2∘h^op
...
-- 텍스트에 따라 아예 h: Y -> X로 뒤집어 두고 설명을 시작하기도 합니다. 그러면
g1 ----> g1∘h
g2 ----> g2∘h
...또는 다음처럼 볼 수 있습니다. 이미 모피즘들은 반대op 방향 모피즘을 모두 가지고 있습니다. 그들 중 어떤 것과 짝을 지어 줘야 구조가 보존되는가를 보면 됩니다. 위에는 보통의 펑터도 F^op가 같이 있는 상황에서 매핑을 대상을 고르는 것이고, 아래는 홈펑터 얘깁니다. 함수형에서는, 모든 데이터들이 그 때 그 때 생성이 아니라, 마치 예정된 미래처럼 모두 있다고 생각하는 게 도움이 될 때가 있습니다.
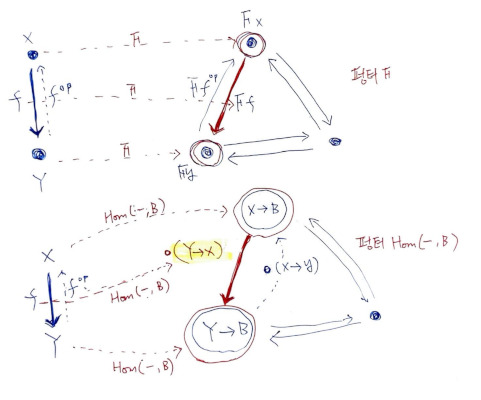
※ 파란색 굵은 화살표와 빨간색 굵은 화살표를 매핑하는 게 목표입니다.
∘ (X->Y)도 있고, ∘ (Y->X)도 이미 존재하는데, X->Y 모피즘의 구조를 보존하려면, 어느 것과 매핑해야 구조가 보존되는가입니다. X->B에서 Y->B로 연결, 혹은 변환되어야 합니다. ∘ (Y->X)를 붙여 Y->X->B로 변환합니다.
대상을 깰 수는 없습니다. 대상이 함수라면, 입력 쪽에 있는 것에 영향을 미치려면 먼저 영향을 줘야 하고, 출력 쪽에 있다면 나중에 영향을 주는 수 밖에 없습니다. (X->Y)이 한 덩어리로 대상입니다.
입력에 두는 것이 Contravariant가 필요하게 되는 게 오묘합니다. 최종 결과 모양이
Y->B로Y가 입력에 있는 걸 원하니,∘ (Y->X)가 필요한 게 당연하긴 한데, 여전히 속 뜻이 더 있지 않을까 싶습니다.상상
X를X->X항등 함수로,Y를Y->Y항등 함수로 두면 (모든 걸 Computation으로 두면) 그동안 편하게 해오던,f:X->Y를X에 적용해서Y가 되는 건,f:(X->X)->(Y->Y)으로 두면,Id_X:X->X가 변환되어 최종 모양이Id_Y:Y->Y가 되어야 하기 때문에Y->
X ---> X->X ---> X->Y
Y -------------------> Y로 볼 수 있습니다.
X에서Y가 아닌 ,Id_X가Id_Y로 변환되려면(혹은 매핑하려면) Contravariant인Y->X, Covariant인X->Y가 모두 필요합니다.
Id:X->X를 변환해서X->Y로 만든다면, Contravariant를 없애고,
Id:X->X를 변환해서Y->X로 만든다면, Covariant를 없앱니다.Contravariant Covariant X->X ---> X->Y ----------> X->Y Y->X ---> X->X ----------> Y->X대상 속에
->가 있다면(모든 게 Computation인 세상이라면), “Contravariant는 항상 따라다니고 있던 것이었다”라고 상상해 봤습니다.
※Id_X가Id_Y로 가려면,Y->X,X->Y가 있어야 합니다. Adjunction으로 생각이 이어집니다.
a->b는a라는 기준점을 봤을 때b로 가는 길Computation입니다.a를 바꾼다는 건, 자로 길이를 잴 때 기준점을 바꾸는 것과 동일한 동작입니다. Contravariant합니다.
※ 모피즘 매핑을 보면 X -> Y에 펑터를 적용한 결과가 방향이 뒤집어진 Y -> X여서 Contravariant 펑터입니다. 입력이었던 것이 출력이 되고, 출력이었던 것이 입력이 되었습니다.
참고 - Covariant, Contravariant, Positive, Negative
첫 번째 인자를 고정하면 Covariant 펑터를 주고, 두 번째 인자를 고정하면 Contravariant 펑터를 줍니다. (위 설명하고 헛갈리지 말아야 합니다. variant한 값이 어디 있는지를 봐야 합니다.)
Hom(A, -), Hom(-, B)는 다음과 같은 가환 다이어그램이 성립합니다. f: B -> B', h:A' -> A에서 아무거나 짝지으면 ※ 위키 Hom functor에서 발췌
Hom(A,B) -----Hom(h,B)-----> Hom(A',B) -> Hom(-,B) 변환
| |
| Hom(A,f) | Hom(A',f)
| |
V V
Hom(A,B') ----Hom(h,B')----> Hom(A',B') -> Hom(-,B')로 변환
| |
V V
Hom(A,-)로 변환 Hom(A',-)로 변환양 쪽 경로 모두 g:A -> B를 f∘g∘h:A' -> B'로 보냅니다. (※ 하나는 Covariant, 하나는 Contravariant로 정의한 덕에 f∘g∘h 모양으로 합성할 수 있게 됐습니다.) 이 가환이 갖는 의미가 뭘까요? Covariant 펑터 Hom(A,-)를 적용한 후에 Contravariant 펑터 Hom(-,B)를 적용하나, Contravariant 펑터를 적용 후 Covariant 펑터를 적용하나 결과가 같습니다. 이 걸 Natural Manner라고 부릅니다.
두 펑터를 합친 Hom(-,-)는 바이펑터bifunctor입니다. C카테고리에서 한 번만 뽑는게 아니라, 두 번 뽑아아야 하니 C × C에서 Set으로 가는 바이펑터인데, 첫 번째 인자를 고정하면 Covariant하고, 두 번째 인자를 고정하면 Contravariant합니다.
Hom(-,-): C^op × C -> SetC^op는 C의 화살표를 모두 뒤집어 놓은 반대opposite 카테고리입니다.
※ “C × C -> Set인 바이펑터로, 첫 번째 인자에 Contravariant하고, 두 번째 인자에 Covariant하다”라고 말로 쓰거나, C^op × C -> Set 이렇게만 표기하거나 하는 것 같습니다 (검증필요)
※ 바이펑터는 적용할 대상도 2튜플로 받고, 결과도 2튜플로 내뱉습니다.
C^op × C product 카테고리에서 대상 (X, Y)의 매핑은,
(X, Y) —바이펑터(A를 고정한 펑터 Hom(A,-), B를 고정한 펑터 Hom(-,B)—> (Hom(A,X), Hom(Y,B))
모피즘 매핑은
(f, h) —바이펑터(A를 고정한 펑터 Hom(A,-), B를 고정한 펑터 Hom(-,B)—> (Hom(A,f), Hom(h,B))
상상 @todo
C와 D가 같은가를 볼 때,C와D의 대상을 사람이 눈으로 확인하듯 보는 게 아니라,C와D사이를 오가는 펑터가id펑터들과 같은가를 봤습니다. 둘이 같은가를 표현하는데, 대상은 등장하지 않습니다. 펑터만 보면 됩니다. 어떤 펑터와 어떤 펑터가 닮았는지, 같은지를 보면 됩니다. identity를 확인하는데, 주변과의 관계만 얘기하고 있습니다.대상
A의 정체성?은 뭘까요? 대상A는 무엇이다라고 결정하는 게 사실은 주변과의 관계로 결정됩니다. 카테고리가 동형인가를 보기 위해 펑터를 보듯, “대상이 무엇이다”라고 말하는 건, 한 대상이 다른 대상과 맺는 관계, 즉 모피즘들을 훑어 보면 됩니다. 홈펑터는 이 걸 뜻합니다.Naturality Condition(Square)
C->D인F펑터와G펑터가 Naturality Condition(Square)을 만족한다고 하면, 이 걸로 뭘 알 수 있을까요?F와G모두C의 구조를 보존한 채로D에 상image을 만듭니다. 이 두 상은 적어도 일부 구조는 같습니다.(보존 됐습니다.)
:렘마, 레마, 레머… 음차로 쓰는 말이 여럿인데, 여기선 보조 정리라 부르겠습니다.
이제 요네다 보조 정리를 볼 준비가 끝났습니다. 짧은 지식에 카테고리 이론의 정수 중 하나라는 요네다 보조 정리를 꾸역 꾸역 이해하려고 하는 이유는, Lens 때문입니다. Lens에서 get, set 인터페이스를 하나의 형태로 통일하기 위해 쓴 “테크닉”이 바로 요네다 보조 정리라 하니, 궁금해서 붙들고 있습니다. (참고 - 요네다 보조 정리에 대해 전혀 모를 때 쓴 글입니다. Lens - 펑크터의 독특한 활용)
또 다른 표기:
H_A = Hom(-, A) Contravariant 펑터
H^A = Hom(A, -) Covariant 펑터
※ ^A는 윗 첨자, _A는 아래 첨자. (홈펑터의 홈셋을 얘기할 일이 있어, 혼동을 줄이기 위해 좀 더 간결한 표현이 필요했을 거라 추측합니다.)
아래는 요네다 보조 정리의 특수한 경우라 할 수 있는데, 일단 이 것부터 보겠습니다.
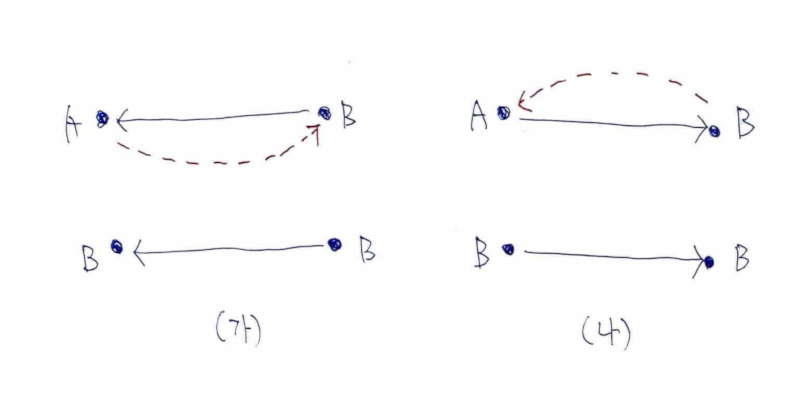
(가) Hom(H_A, H_B) ~= Hom(A, B)
(나) Hom(H^A, H^B) ~= Hom(B, A)왼 쪽, 오른 쪽 Hom의 의미가 다릅니다. 오른 쪽은 모피즘 집합을 의미하고, 왼 쪽은 펑터에서 펑터로 가는, 즉 자연 변환Natural Transformation 집합(펑터 사이의 모피즘이 자연 변환이니, 모피즘 집합이라 불러도 됩니다.)입니다.
“A->B모피즘은 Hom(-,A) -> Hom(-,B) 자연 변환과 동형isomorphic이다.”
홈펑터 정의를 그대로 넣어, 직관적으로 따라가 보겠습니다.
Hom(-,A)홈펑터는
X1 ---> Hom(X1,A)
X2 ---> Hom(X2,A)
…
Hom(-,B)홈펑터는
X1 ---> Hom(X1,B)
X2 ---> Hom(X2,B)
…
머리가 복잡한데, 원래의 모피즘 A->B를 잠시 X->Y로 두겠습니다.
Hom(-,A)홈펑터가 X->Y를 매핑한 모피즘은 Hom(X,A) -> Hom(Y,A)입니다.
X->A를 Y->A로 변환하려면, Contravariant하게 ∘(Y->X)를 쓰면 됩니다.
(X->A)∘(Y->X) -- Y->X->A -- Y->A같은 작업을 Hom(-,B)에도 하면
(X->B)∘(Y->X) -- Y->X->B -- Y->BY->A와 Y->B의 차이는 A->B입니다.
Y->A->B
둘 간의 차이, 즉 Hom(-,A)홈펑터에서 Hom(-,B)홈펑터로 가는 자연 변환은, Y->A 후에 A->B를 하면 Y->B가 되니 A->B가 바로 자연 변환입니다. 두 홈펑터 사이의 자연 변환도 (A->B)∘가 나왔습니다. Y가 B인 경우를 보면,
B->A->B
B---->B
※ 1과 2의 차이는 +1이라고 말하듯, B->A와 B->B의 차이(자연변환)는 A->B((A->B)∘)입니다. 이런 결과가 나오는 게 당연해 보이기도 하고, 신기하기도 합니다.
“B->A모피즘은 Hom(A,-) -> Hom(B,-) 자연 변환과 동형isomorphic이다.”
Hom(A,-)홈펑터는
X1 ---> Hom(A,X1)
X2 ---> Hom(A,X2)
…
Hom(B,-)홈펑터는
X1 ---> Hom(B,X1)
X2 ---> Hom(B,X2)
…
역시, 원래의 모피즘 A->B를 잠시 X->Y로 두겠습니다.
Hom(A,-)홈펑터가 X->Y를 매핑한 모피즘은 Hom(A,X) -> Hom(A,Y)입니다.
A->X를 A->Y로 변환하려면, Covariant하게 (X->Y)∘를 쓰면 됩니다.
(X->Y)∘(A->X) -- A->X->Y -- A->Y같은 작업을 Hom(B,-)에도 하면
(X->Y)∘(B->X) -- B->X->Y -- B->YA->Y가 B->Y가 되려면 ∘(B->A)이 있으면 됩니다.
B->A->Y
두 홈펑터 사이의 자연 변환은 ∘(B->A)가 됩니다. Y가 B인 경우를 보면
B->A->B
B---->B
위에서는 Hom(-,A) -> Hom(-,B)만 봤지만, Hom(-,B)자리에 C^op -> Set 모양의 어떤 펑터든 성립한다고 합니다. 이를 식으로 쓰면, (※ 상상 - 카테고리 Set의 대상이 어떤 set인지는 보지 않고, Contravariant하기만 하면 동작이 성립할테니, 당연히 그럴 것 같긴 합니다.)
※ 위의 경우는 요네다 보조 정리의 C^op -> Set 자리에 Hom(-,B)를 넣은 특수한 경우입니다.
A -> Hom(-,A)
B -> Hom(-,B)
...이렇게 매핑하는 걸 요네다 임베딩embedding이라 부릅니다. Set 카테고리에 A와 대응하는 집합, B와 대응하는 집합, … 들을 모두 모아서 보면 Set 카테고리에 현재 카테고리 C와 대응되는 상image을 만든다고 볼 수 있겠습니다.
F펑터: C^op -> Set일 때,
Hom(-,A)홈펑터 -> F펑터 자연 변환이 F(A)와 (일대일 대응bijection | 동형?)
Nat(Hom(-,A),F) ~= F(A)위 식이 성립한다가 요네다 보조 정리입니다. 좀 더 정확히는
“F가 locally small category C에서 Set으로 가는 펑터일 때, C에 있는 각 대상 A에 대해, h_A에서 F로가는 자연 변환 Nat(h_A,F) ≡ Hom(Hom(A,-),F)는 F(A) 원소와 일대일 대응이다.”
※ Hom이라 써도 되지만, 자연 변환임을 드러내기 위해 Nat가 더 적당해 보입니다.
Let
Fbe a functor from a locally small categoryCtoSet. Then for each objectAofC, the natural transformationsNat(h_A,F) ≡ Hom (Hom(A,−),F)fromh_AtoFare in one-to-one correspondence with the elements ofF(A).
※ Nat(Hom(-,A),F)와 F(A)는 동형isomorphic이다라고 해도 될 것 같은데, 일대일 대응을 먼저 짚어 줍니다. 수식에는 동형(~=)이라 해놓고 설명 문장에는 일대일 대응이라 하는데 다른 이유가 있는지 잘 모르겠습니다. (자연 변환이라 일대일 대응만 봐도 동형이 되기 때문일거라 추측하고 있습니다.)
아주 추상적으로 어떤 정보를 가지고 있는지 살펴 보는 게 도움이 될 때가 자주 있습니다. 위 식에서 왼 쪽이 가지고 있는 정보는 A를 표현하는 다른 방법으로 A를 표현하고 있고, F를 가지고 있습니다. 오른 쪽도 F와 A를 가지고 있습니다. 둘이 동형에 가까울 거라 예측해 볼 수 있는 대목입니다.
저는 함수를 차이로 해석하기도 하는데, Hom(-,A)와 F의 차이를 나타내는 자연 변환과 F A가 같다고 직관적으로 읽히기도 합니다.
눈에 보이는대로 해석해 보면,
F를 대상A에 적용:F:_ -> 구현을 A에 적용하면 A -> 구현이 됩니다.F를 A를 가진 홈펑터와 차이로 변환:Hom(_,A)와 F의 차이, 즉 자연 변환 Φ는 _ -> A와 _ -> 구현의 차이니 (A -> 구현)∘이 됩니다.Φ에는 이미 _->구현도 A도 미리 들어가 있습니다.
f
A ----------------> X
Hom(A,f)
id_A = Hom(A,A) ----------------> Hom(A,X) = f
| |
Φ_A | | Φ_X
v v
F A ----------------> F X
= u F f대부분의 텍스트들이 어째서 u만 결정되면, 위 가환 다이어그램이 완전히 정해지는지 후루룩 얘기하고 넘어 갑니다. 여러 텍스트를 봐도 이해가 잘 안가, 역시나 상상을 곁들여 쫓아가 봤습니다.
F X = ( F f) u -- 아래 쪽 경로
F X = (Φ_X f) -- 오른 쪽 경로우선 보이는 대로, 제 방식대로 직관적으로 읽으면, f를 F로 변환한 것과, f를 Φ_X로 변환한 것의 차이는 u입니다. u가 isomorphism에서 어떤 역할을 할 것 같이 보이는 대목입니다.
※ 여러 개의 텍스트를 동시에 보다 보니, 표기가 마구 섞여 있습니다. Hom(-,A)에 대한 것을 모두 확인했다면, Hom(A,-)는 화살표만 모두 뒤집으면 그대로 성립하는 듀얼이라 합니다. 듀얼에 대한 심상이 아직 명확하지 않지만, 어쨌든 한 쪽을 알면, 간단히 다른 한 쪽도 알 수 있어서, 그 때 그 때 필요한 걸로 설명을 풀어가고 있습니다.
좀 더 자세히 해석해 보겠습니다. (검증 필요)
목표는 Φ와 F가 일대일 대응인지를, 즉 Φ가 정해지면 유일한 F가 정해지고, 거꾸로 F가 정해지면 유일한 Φ가 정해지는지를 봅니다.
F:C -> Set임을 상기하고,
우선 F A에 있는 원소에 Φ로 매핑하는 걸, 적어도 하나는 찾을 수 있습니다. Φ의 A성분 Φ_A는 어찌되나 보면,
Φ_A: Hom(A,A) ------> (F A)로 변환합니다. A->A인 모피즘으로 id_A는 항상 존재하니, id_A와 대응 되는 Φ_A(id_A)가 F A에 존재합니다.
Φ_A(id_A) ∈ F A이제 F A의 원소들을 u1, u2,… 라 하면, 이 중에 Φ_A(id_A)가 되는 u_가 있을테고, 이 u_가 유일한 자연 변환 Φ와 대응된다면, u만 정해지면 위 가환 다이어그램이 결정된다고 볼 수 있습니다.
홈펑터 Hom(A,-)와 F 펑터로 Naturality Condition을 보면, 위 가환 다이어그램이 나옵니다. 가환 다이어그램을 잘 쫓아가 보면, 여기에 Φ_A(id_A) = u(왼 쪽 아래 F A)가 있습니다.
상상 - Φ2: Nat(Hom(B,-), F)나 Φ3: Nat(Hom(C,-), F)…등의 가환 다이어그램은 Φ2_A(id_A), Φ3_A(id_A) 정의가 없습니다. Φ_A(id_A) = u를 찾는 다면 유일하게 Φ: Nat(Hom(A,-),F)를 고를 수 있습니다.
F A의 원소 중 u만 정해지면 Φ가 결정됐습니다. 목적지에 도달했습니다.
위 다이어그램은 F, A에 대해서 Natural 합니다. 특정 F여야만, 특정 A여야만 성립하는 것이 아니란 말입니다. C->Set인 어떤 F를 받아도 성립하는 건 알겠는데, A는 Hom(A,-)로 정해진 게 아닌가 생각했습니다. 제대로 람다식은 아니지만, 마치
\F A -> Nat(Hom(A,-),F) = F A이렇다는 말입니다. F는 펑터니, 모든 대상에 정의될테고, 그런 F를 고르고, 아무 대상 A를 골라도 이 식은 성립한다는 얘깁니다. Natural이란 말을 언제 쓰나 살짝 모호한감이 있었는데, 이런 의미인가 봅니다.
대상이나 모피즘이 아닌, 위 가환 다이어그램 자체를 하나의 단위 오브젝트처럼 생각할 수 있겠습니다. F, A가 결정되면 Naturality Condition(자연 변환의 가환 다이어그램)이 결정됩니다.
내가 관심 갖는 대상은 B라 했을 때, 이 B를 F로 옮기면, F B가 됩니다. Hom(B,-)는 이 B와 연관된 모피즘을 의미합니다. 자연 변환은 각 성분을 보는 게 도움이 될 때가 많습니다. 위 Naturality Condition은 B와 연관된 모든 모피즘에 F를 먼저 적용해 옮겨버릴 방법을 미리 준비하는 것과, F로 옮긴 상태의 관계입니다. 각 대상과 모피즘에 동작할 F의 성분들을 미리 변형해 둔 것과, 그냥 F B 를 한 상황에서 다른 모든 대상들과 관계를 표현한 Hom(F B,-)를 보면 같다는 뜻입니다. 비유해서 그리면
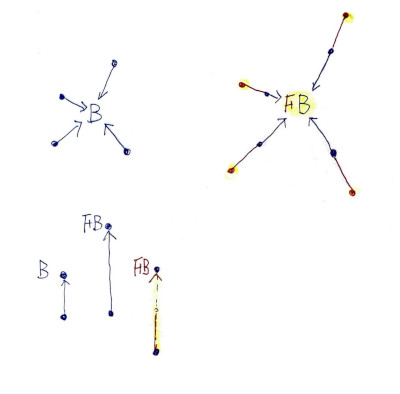
두 점이 있는데, 한 점을 멀리 옮긴(F) 다음에 선을 긋든(홈펑터), 미리 선을 길게해서(홈펑터와 F의 자연변환) 준비해서 두 점 사이에 놓든 결과는 같습니다. 비유하자면, 자의 눈금을 바꾸고 쟀다거나, 기준점을 옮겼다고 상상해 볼 수 있습니다. 공부하면서, 중간 중간 혼동했는데, 화살표를 늘리는 “동작”과 결과 값인 “F B”가 같다가 아니라, 일대일 대응시킬 수 있다는 얘기입니다.
저는, ““내가 움직여서 내가 뭔가를 만들어내서 변한다면 Covariant하지만, 나는 가만히 있는데, 남이 무언가 만들어서(주변이 변해서) 내가 변한다면(변한 것처럼 된다면) Contravariant”란 심상을 가지고 있습니다.
요네다는 이런 아이디어를 완벽하게 수식으로 기술하고 있습니다. 홈펑터 아이디어 형식화부터도 신기한데, 여기에 펑터 적용한 게 원래의 것과 일정하게 대응되는 걸 보니 아름답네요. 카테고리란 체계를 만든 게 이런 아이디어를 표현하는데 딱일 것을 미리 상상했을까요. 천재들의 머릿속은 알 수 없으니, 감탄만 하고… 잘 써먹으면 됩니다.
※ 단순히 화살표를 확장시키는 건,
F가 엔도 펑터가 아닌데, 오해를 살 수 있다 지적해주셨습니다.
이에 부연 설명을 하자면,B를 가리키는데는 주변 화살표의 “길이”로B를 특정 짓는다고 가정해 보겠습니다.F펑터로 다른 카테고리로 보냈더니, 화살표의 길이가 달라졌습니다.h_B: Hom(-,B) Φ: h_B->F 자연변환 f_A: A->B 모피즘 f_B: B->B 모피즘 f_C: C->B 모피즘 ... ((Φ_A(h_B))f_A)A = F B ^^^^^^^^^^^^^^^^ f_A변환 ((Φ_B(h_B))f_B)B = F B ^^^^^^^^^^^^^^^^ f_B변환 ((Φ_C(h_B))f_C)C = F B ^^^^^^^^^^^^^^^^ f_C변환이렇게
C카테고리에 있던A->B,B->B,C->B모피즘들이Set카테고리로 옮겨가면서 변환되는 걸 은유했습니다. (아주 특수한 경우로,Set로 가면서 오브젝트들과 멀어졌다는 상상을 했습니다.)“
B가 무슨 역할을 할지를A,C와의 거리로 표현(은유?상징?)한다면,
B를 움직이든,B는 가만히 두고A,C를 벌리든 같은 정보를 표현할 수 있다”로 요네다 정리를 이해하고 있습니다.
생각 스트레칭 - 상상
예를 들어 func(f) = f x의 구현을 결정 짓는 건 x에 달려 있습니다. f부분은 이 func의 특징이 아닙니다.
func1(f) = f 1, func2(f) = f 2, … 이렇게 되어 있다면, x=1이라면 func1을 고를 것이며, x=2이라면 func2를 고를 것입니다. 다시 말해, x만 정해지면 func1, func2,…들 중에 무엇을 고를지 결정됩니다. 모피즘 func~와 대상x는 일대일 대응입니다. (f가 정수를 받는 함수라는 제약이 있긴 하지만, 여기선 이 게 func1과 func2의 구별 요소는 아니라는 얘깁니다.)
1 --> func1
2 --> func2
...
a --> \f = f a (F f) u = Φ_X f
이 식에서 f와 X는 외부에서 나중에 들어 올, 위 예시의 고차 함수가 같은 것들입니다. 이 식을 결정하는 건 u입니다.
여기 저기 텍스트를 찾아 다녔는데, 위 가환 다이어그램만 써서 증명이 끝나는 곳도 있고, 각 펑터로 바라보고 Natrual isomorphic을 확인해서 증명하는 곳도 있는 듯 합니다.
※ 첫 눈에는 자연 변환과 대상이 같다로 오해했는데, 같다가 아니라 동형입니다.
Φ: Nat(Hom(A,-),F)는 u=F A와 같다(=)가 아니라, 동형(~=)입니다.
α: Φ -> u
β: Φ <- u 두 함수가 있고, 이들을 합성해서 α∘β = id_Φ, β∘α = id_u가 되는 걸 보여야 Φ와 u, 즉 F A가 동형임을 보이게 됩니다.
우선 α부터 보겠습니다.
>haskell α : Nat(Hom(-,A),F) -> F(A)
Hom(-,A) F(A)
(A->A)와 F의 차이 -> u1
(B->A)와 F의 차이 -> u1
(C->A)와 F의 차이 -> u1
...
Hom(-,A) F(A)
(A->A)와 F의 차이 -> u2
(B->A)와 F의 차이 -> u2
(C->A)와 F의 차이 -> u2
...
...u가 정해지면,Φ 가환 다이어그램으로 위 그룹 중 하나를 특정지을 수 있습니다.
트릭으로 (A->A)로 id_A는 항상 존재하니, 가장 만만한 (A->A)를 골라서 보겠습니다.(A를 고르는 이유 검증 필요)
α = \Φ -> Φ_A(id_A) -- Φ ↦ Φ_A(id_A) 자연 변환 Φ에 id_A를 넣어 주면 F A를 알 수 있습니다. 만일 (B->A)인 어떤 모피즘을 넣어 준다해도, id_A일 때 나온 F A와 같아지는 Φ일테니, 무엇을 넣든, id_A로 결정된 F A는 바뀌지 않습니다. 한 마디로 Hom(-,A)에 속한 모피즘들 중 아무거나에 Φ를 적용하면 F A를 알 수 있는데, 그 중 가장 단순한 id_A를 넣고 있습니다. (Φ는 성분별로 봐야되는 걸 떠올리면 이해에 도움이 됩니다.)
이제 β: u -> Φ를 보겠습니다.
u = F A를 선택하면 유일한 Φ가 결정되어야 합니다.
이미 이전 섹션에서 가환 다이어그램이 F A로 결정된다는 걸 보았습니다.
\u -> (F f) u = Φ_X(f) 가환 다이어그램이 결정된다.
^^^^^^^^^^^^^^^^
Φ를 특정지을 수 있는 속성이 걸로 증명을 마무리하는 텍스트들이 많은데, 전 Natural isomorphic을 보는 쪽이 더 명확하게 보였습니다.
Category Theory II 4.2: The Yoneda Lemma 영상에서 보여주는 증명을 따라가 보겠습니다.
Nat(Hom(A,-)와 F A가 동형인가를 보기 위해, 둘이 자연 동형Natural isomorphic인지 보는 방법입니다.
(@Ailrun님이 해석 방법을 알려주셨습니다. 감사합니다.)
둘이 자연 동형인지 보려면 둘의 공통 근원이 되는 게 있어야 합니다.
(※ 대소문자 표기와, 홈펑터 표현들이 좀 다른데, 여기선 위 영상을 따라 가겠습니다.)
F a를 F:[C,Set]와 a:C를 받아서 Set를 만드는 펑터로 봅니다.
F a : [C,Set] × C -> SetΦ:[C,Set](C(a,-),F)도 마찬가지로 봅니다. 자연 변환이지만, 여기서는 Set로 가는 펑터로 보고 있습니다.
[C,Set](C(a,-),F) : C × [C,Set] -> Set영상에서는 C × [C,Set] -> Set으로 통일합니다.
이제 이 두 펑터가 C×[C,Set]인 (F,a)를 변환하는 걸 Natural Square를 그려서 자연 동형을 확인합니다. 모든 F, a 조합에 Φ와 F a가 자연 동형임을 보이면 증명이 완성됩니다. (F,a)를 Φ펑터를 거쳐 변환된 것과, F펑터를 거쳐 변환된 것(영상에서 이 부분을 Functor Application이라 부르고 있습니다.)의 관계를 봅니다.
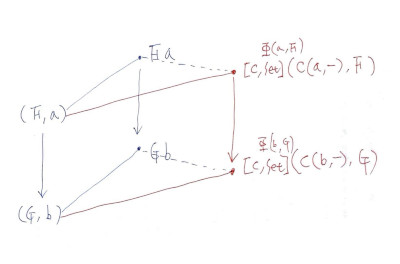
(F,a) -> (G,b)와 F a -> G b를 보겠습니다. (F,a)란 프로덕트 카테고리이니, μ: F->G, u: a->b를 각각 봐서 (μ,u)가 됩니다. F와 G는 펑터이니, 각 성분별로 보면 μ_x: F x -> G x로 표현하고 있습니다. 그럼 F a -> G b는 F a에 μ를 적용해서 G a로 바꾼 후 G의 fmap으로 a를 b로 바꿉니다. G u ∘ μ_x
※ 혹 G u가 어색하다면, 보통 f에 F를 적용해서 F f가 되는 걸, 코드로 생각하면 F f란 F의 fmap으로 f를 변환한 것입니다.
(F,a) - > (G,b)와 [C,Set](C(a,-),F) -> [C,Set](C(b,-),G)를 보겠습니다.
C(a,-), F, G는 펑터니 자연 변환은 성분을 봐야합니다.
α_x = C(a,x) -> F x ---> (a->x) -> F x
β_x = C(b,x) -> G x ---> (b->x) -> G x
(b->x)가 (a->x)가 되려면, u: a->b, μ_x: F x->G x를 써서 μ_x∘α_x∘u
보기 좋게 원래 원했던 식(F f) u ~= ϕ_x(f)과 딱 떨어지는 모양이 나오면 좋겠지만, 증명은 아래와 같이 끝납니다.
(가). (F,a)는 F와 a에만 의존해서 결정되니, (G,b)도 u: a->b, μ:F->G에만 의존해서 표현할 수 있습니다.
(나). F a도 F와 a에만 의존해서 결정되니, G b도 u,μ에만 의존해서 표현할 수 있어야 합니다.
(다). [C,Set](C(a,-),F)도 F와 a에만 의존해서 결정되니, [C,Set](C(b,-),G)도 u,μ에만 의존해서 표현할 수 있어야 합니다.
(가)는 (μF, ua)
(나)는 G u ∘ μ_x
(다)는 μ_x∘α_x∘u
정리하면 F a도 F와 a에만 의존해서 결정되고, Φ: [C,Set](C(a,-),F)도 F와 a만 의존해서 결정되므로 둘은 동형이란 얘깁니다. 수식으로 딱 떨어지는 걸 보고 싶었는데, 영상에선 이렇게 끝을 맺고 있습니다.
더 추상적으로 얘기하면, 함수 두 개 f, g가 f(a,b)로 a, b에만 의존하고, g(a,b)도 역시 a, b에만 의존한다면 둘 사이의 일정한 대응 관계를 만들 수 있습니다. 값이 고정되어 있지 않은 폴리모픽, 즉 forall a, forall b와의 관계에만 의존해서 결과가 결정되는, 둘에게서 (어떤 절차를 거치면) 같은 정보를 뽑아낼 수 있습니다.
a를 b에 적용할 함수(펑터)로 보면, 가장 간단하게 a, b 정보를 가지고 있는 식은 a b 입니다.
도메인, 코도메인이 같은 어떤 두 펑터 F (a -> Fa,f -> Ff)와 G (a -> Ga,f -> Gf)의 자연 변환 성분을 보면
Fa와 Ga의 차이
Ff와 Gf의 차이
입니다. 자연 변환 자체는 a, f에만 의존하고 있습니다.
이 자연 변환이 바로 둘의 일정한 관계를 뜻합니다. 아주 확실한 건 아닙니다만, 아주 아주 축약해서 얘기하면, 요네다는 자연 변환 성질을 얘기한 것인가라는 생각이 듭니다.
C 카테고리 자체가 어떤 복잡한 구성, 구조를 가지고 있든 간에,
[모든 구성원이 a에 의존하게 만드는 펑터(:C->Set)]와,
[임의의 펑터 F:C->Set] 사이의
자연 변환 자체는 F, a에만 의존할 거라 추측할 수 있습니다.
조금 더 복잡하게 얘기하면, 위 자연 변환 자체를 또 펑터로 보고(뎁스가 이렇게 깊어지는 건 저도 별로 안 좋아합니다만, 위 증명을 그대로 쓰면)
[[모든 구성원이 a에 의존하게 만드는 펑터] -> [임의의 펑터 F]] 펑터(여기선 자연 변환이 아닌 [C,Set] × C -> Set펑터)와
[(a,F) -> F a] 펑터
사이에 존재하는 자연 변환을 정의할 수 있으니, [모든 구성원이 a에 의존하게 만드는 펑터]는 a와 동등한 의미를 가지고 있다는 결론에 도달합니다.
너무 결론으로 훅 점프한 것 같긴한데, 조금 더 힌트가 될만한 말을 덧붙이자면, 펑터는 C를 변형하는 동작이지, C가 아닙니다. F를 x에 적용해서 나오는 “값”은 x에 의존하지만, F자체가 어떤 동작을 할지는 x에 의존하는 것이 아닙니다. F i = +i 함수를 x에 적용한다면, x+i가 됩니다. F는 i에 의존해서 동작이 결정되고, 이를 x에 적용합니다. 이 동작만 떼 내어 보는 겁니다. 홈펑터는 홈펑터 a = a ->라는 함수로 보고, 이 홈펑터의 동작은 a에만 의존한다 말하고 있습니다.
요네다 벽을 넘고 나면, 카테고리 이론을 이해하는데 도움이 된다고 하는데, 자연 변환에 대한 인사이트(한 눈에 보이진 않지만, 본질적인 의미)가 생겨서 그렇다는 뜻 아닐까 합니다.
카테고리 이론의 지상 최대 과제는, “모든 것들을 관계로 설명하자”입니다. 요네다는 이 말을 그대로 이론으로 보여주고 있습니다. A에 F를 적용하는 것은 A를 나타내는 Hom(A,-)와 F의 자연 변환으로 대체할 수 있다는 말입니다. 안 그래도 추상화에 추상화로 머리가 터지는데, 애초에 홈펑터로 시작하면 얼마나 복잡할까 싶습니다. 함부로 건드릴 대상은 아니지만, 거의 모든 걸 함수, Computation으로 보려는 하스켈에서 무언가를 같게(동형) 보는 작업은 매우 중요합니다. 현재까지는, 동형으로 보기 위한 3대장 테크닉이 모나드, Adjunction, 요네다 정리로 생각됩니다. 모나드를 제외하면 직접적으로 쓸 일이 많지 않겠지만, 현실을 모델링할 때 영감을 주는 역할을 할 수 있을거라 믿습니다.
※ 지금은 설명할 정도로 잘 알지 못하지만, 어렴풋이 셋의 연결 고리가 보입니다.
Icelandjack/Yoneda_II.markdown
scturtle.me - yoneda
from Lenses to Yoneda embedding - 바르토즈 밀레프스키
아래 코드는 Understanding Yoneda - 바르토즈 밀레프스키에서 발췌했습니다.
{-# LANGUAGE ExplicitForAll #-}
imager :: forall r . ((Bool -> r) -> [r])
imager = ???
data Color = Red | Green | Blue deriving Show
data Note = C | D | E | F | G | A | B deriving Show
colorMap x = if x then Blue else Red -- Bool -> (r=Color)
heatMap x = if x then 32 else 212 -- Bool -> (r=Int)
soundMap x = if x then C else G -- Bool -> (r=Note)
main = print $ imager colorMap위 imager 함수를 구현할 때 요네다 보조 정리를 쓰면,
forall r. ((a -> r) -> f r) ~= f a
^^^^^^^^^^^^^^^^
자연변환: Hom(a,-) -> F -바로 a에서 다른 모든 대상 forall r.으로 가는 모피즘의 집합, Covariant 홈펑터 Hom(a,-)입니다.
imager :: forall r .((Bool -> r) -> [r])
-- (고정값 -> r) 펑터[] 요네다 보조 정리에 따라 위 식은 [Bool]과 같은 의미를 가지고 있습니다. 위 서명에 맞게 구현하려면, [Bool]에 따라 고유한 자연 변환 스퀘어가 나온다는 걸 요네다가 알려 줍니다. 예를 들어 [True, False, True, True] 이런 값이 있다면, 이에 대응하는 자연 변환은 한 가지 뿐입니다.
반대로 imager이 갖고 있는 [Bool]을 찾고 싶다면, Bool -> r자리에 id 를 넘겨주면 됩니다.
홈펑터부터 살펴 보겠습니다. 아래 그림에서 모피즘도 봐야되지만, 펑터들의 차이를 보기 위해 대상이 변환되는 것만 보겠습니다.
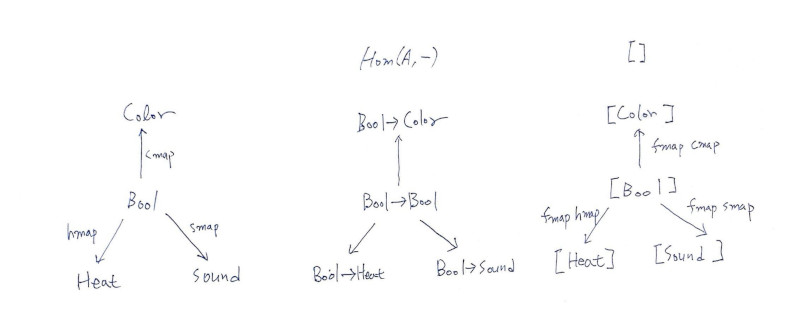
imager :: forall r . ((Bool -> r) -> [r]) -- 자연 변환
-- 홈펑터 F
imager iffie = fmap iffie [True, False, True, True] -- 자연 변환이 [Bool]을 가지고 있다.
idBool :: Bool -> Bool
idBool x = x
main = print $ imager idBoolF: C -> Set인 어떤 펑터든 Hom(A,-)홈펑터와 자연 변환을 생각해 볼 수 있습니다. 마치, 홈펑터를 기준으로 삼고, 다른 펑터들을 갖다 대서 비교해 본다고 생각할 수 있습니다. 여기선 리스트 [] 펑터로 예를 들고 있습니다.
※ 마치 기준점이 0일 때 3이면, 기준점을 1로 옮기면 2라는 값으로 Contravariant하게 바뀌는 것과 비슷합니다. HomFunctor로 기준점을 바꿔 놓는 걸로 비유할 수 있습니다.
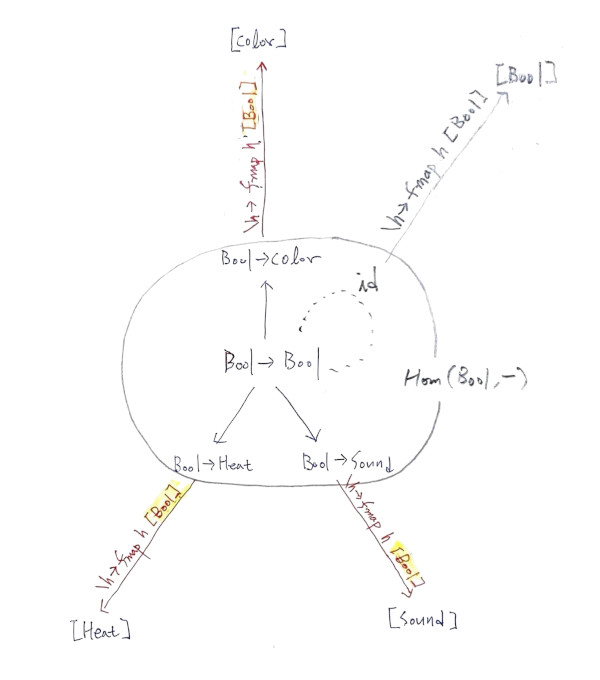
Nat(Hom(A,-), F)가 딱 F a가 나와야만 할 것처럼 오해할 수 있습니다. 딱 F a가 나오는 것은 아니고, up to isomorphism 동형입니다. 자연 변환으로 변환한 펑터가 적용된 값이 아니라, 자연 변환 자체가 F a와 대응한다는 말입니다. 위 그림에서 \h->fmap h [Bool]이 자연 변환입니다. 이 자연 변환은 [Bool]과 일대일 대응할 수 있습니다.
[True]라면 \h->fmap h [True]
[True,False,True,False,True]라면 \h->fmap h [True,False,True,False,True]와 대응합니다.
자연 변환은 F a에 의해서 결정됩니다.
a에 F를 적용해서 F A
Hom(a,-) 펑터와 F펑터의 차이(자연 변환)
어째서 위 두 개가 같은 정보를 담을 수 있을까요? (두 개는 동형 up to isomorphism 입니다.)
필요한 것은 F와 a입니다.
a를 가리킬 수 있는 다른 표현, Hom(a,-)는 a와 (자신 포함) 모든 대상들과의 관계로 a를 가리킬 수 있습니다. 그럼 a에 F를 적용하듯, Hom(a,-)에도 F를 “적용”하는 것과 비슷한 동작을 찾아봐야 합니다. 그래서 동일하게 F a와 동형인 결과가 나오는지 확인해야, Hom(a,-)가 정말 a를 가리키는 또 다른 표현으로 받아들일 수 있습니다.
Hom(a,-)는 모든 대상을 a와 연관 짓습니다. 이 걸 다른말로 하면, 모든 대상을 a를 받는 함수로 만든다는 말입니다. 그냥 b,c,…로 있던 대상들을 a->b,a->c,…로 a를 받아야만 값이 되도록 모두 바꿔 놓았습니다.
b를 홈펑터 Hom(a,-)로 변환한 값은 a를 필요로 하는 a->b이지만, 펑터F로 변환한 값은 F b입니다. 이 때 두 펑터의 차이를 구한다면, 즉 Hom(a,-)를 거친 후 F a에 도달하려면 어떤 과정을 거쳐야 하는지 본다면,
“어디엔가는 a가 있어야만 합니다.”
Hom(a,-)에는 a가 있지 않습니다. a를 받을 수 있지, 가지고 있지는 않습니다. 이 펑터가 F a에 도달하려면, 결국 Hom(a,-)와 F의 자연 변환이 a를 가지고 있어야만 합니다. 대상을 모피즘 집합으로 표현하면서, 원래 대상은 자연 변환에 담아 뒀습니다.
요네다를 모를 때, 프로그래머 지식으로 Contravariant를 해석한 직관이었는데, 요네다 동작을 살필 때도 떠올려 볼만합니다.
이제, 이런 결과를 Lens에 어떻게 적용하는지 볼 차례입니다. 많은 내용을 그대로 얘기해야 하니 Lens 정의에 왜 펑터가 들어가 있을까요?를 같이 봐주세요. 링크 글에서는 요네다 보조 정리를 모르는 상황에서 코드만으로 따라 갔는데, 이제 요네다 보조 정리를 알고 있는 상태에선 어떤 식으로 접근하는지 살펴 보겠습니다.
type LensModify s a = (a -> a) -> (s -> s)
type LensGetter s a = s -> a둘을 모양이 비슷하게 보려합니다.
“A->_와 B->_의 차이는 ∘(B->A)”이다는 요네다 임베딩을 적용하면, (B를 s로, A를 a로)
(g:a -> _)가 (s -> _)가 되려면 ∘(h:s -> a) 필요합니다.
그럼, 아래 모양을 같게 볼 수 있나라는 문제에 도달했습니다. (다른 텍스트를 보고 해석한 것이 아니라 저 혼자 추측이라 아직 확실하진 않습니다.)
type LensModify s a = (a -> a) -> (s -> s)
type LensGetter s a = (a -> _) -> (s -> _)
-- ^^^^^^^^^^^^^^^^^^^^
-- (a->s)와 (s->s)의 차이는 (s->a)입니다. 이제 GHC한테 맡길 방법을 찾아야 합니다. 아래와 같이 멀쩡한 타입에다 폴리모픽 펑터를 붙입니다.
type LensModify s a = (a -> f a) -> (s -> f s)
type LensGetter s a = (a -> f a) -> (s -> f a) -- _ 자리에 f a를 넣었습니다.f를 폴리모픽하게 두고, GHC가 채워넣게 해서 어쩔 땐 a를, 어쩔 땐 s를 고르게 한다면, 하나의 모양으로 표기할 수 있습니다. (물론, f안의 값을 보기 위해 패턴매칭을 하는 run f과정이 필요하지만 가지고 있는 정보 자체는 달라지지 않습니다.)
펑터 타입을 열어 둔
type Lens s a = forall f . Functor f => (a -> f a) -> (s -> f s)를 만듭니다. 하지만 타입을 잘 보면 문제가 한가지 있습니다.
LensGetter의 끝 부분을 보면 f a인데, 추상화한 타입 Lens의 끝 부분을 보면 f s입니다. 이대로는 추상화가 되지 않습니다. 이 부분을 해결하는 트릭이 번뜩입니다.
아래는 아무리 요네다를 알고 있었다해도 어떻게 이런 걸 떠올렸지 싶은 트릭입니다.
newtype Identity a = Identity { runIdentity :: a } deriving Functor
newtype Const a b = Const { getConst :: a } deriving Functor
type LensModify s a = (a -> Identity a) -> (s -> Identity s)
type LensGetter s a = (a -> Const a a) -> (s -> Const a s)요네다 임베딩으로 보면 (a -> _) -> (s -> _)에서 _부분에는 뭐가 들어가도, 같은 게 양쪽에 들어가면 상관없습니다. Lens에 f로 Const a를 넣고, 나중에 runConst를 거치면, 원하는대로 (a -> a) -> (s -> a)가 나옵니다.
이제 GHC가 컨텍스트에 따라서 Identity 또는 Const a를 선택하게 하는 일만 남았습니다.
출력값은 아무 것이나 같기만 하면 된다는 말이 혼동되어 아무 펑터나 되는 것인가 궁금하다면 Const대신 Maybe를 한번 넣어서 확인하면 됩니다.
type LensGetter s a = (a -> Maybe s) -> (s -> Maybe s)runMaybe가 없긴 하지만, 어찌해서 Maybe를 떼어냈다 해도 (a -> s) -> (s -> s)입니다.
Const a는 a를 가지고 들어가는 트릭이 있습니다.
직관적으로 보면, 이렇게 간단히 해석되기도 하는데, Twan van Laarhoven equivalence를 따져서 Lens 분석을 하는 글이 있습니다. 혹시 이 글에서 위 트릭에 관한 이론이 있을지 찾아봐야겠습니다. @todo
@todo Lenses, Stores, and Yoneda - 바르토즈 밀레프스키 글을 해석 중입니다. - Lens와 요네다 보조 정리
The Lens Library
홈펑터 - 위키백과
요네다 보조정리 - 위키백과
The Yoneda Embedding Expresses Whether, What, How, Why - 여기 글을 거의 다 작성했을 무렵 찾은 영상인데요, 다른 영상보다 제 입맛에 맞는 설명입니다. 정의만 읊어주는 영상들은 도통 이해하기 어렵습니다.
Hom functors and a glimpse of Yoneda - 혼란스럽게 쓰이는 기호들을 짚어 줍니다.
수학기록지 - Yoneda Lemma - 드물게 만나는 한글 자료입니다.
Lens Law
Control.Lens.Lens
하스켈 문법만으론 표현할 수 없는 조건을 lens law라 해서 프로그래머한테 떠 넘깁니다. 전 법칙law이 보이면 문법으로 표현, 혹은 강제하지 못하는 조건이 있구나로 생각하고 접근합니다.
view l (set l v s) = v s가 v를 가지고 있게 하고, 거기서 v를 꺼내면 v다.set l (view l s) s = s s에서 꺼내온 값을 다시 s에 넣으면, 그냥 처음과 같은 s다.set l v' (set l v s) = set l v' s v를 넣고, v'를 덮어 씌우면 s가 v'을 가지고 있다.당연한 말 들을 써놓은 것 같이 보입니다만, view와 set이 위 법칙을 지킨다는 건,
v에서 s로 갔다가 다시 v로 돌아올 수 있으려면, set l s 는 모든 s에 대해 단사injective여야 합니다. One to One, 즉 어디서 왔는지 기억해서 돌아 갈 수 있으려면, 하나와 하나만 매핑되어야 합니다.s에서 v로 왔다가 다시 s로 돌아 가려면, set l은 전사surjective여야 합니다. s의 대상들이 빠짐없이 v와 매핑되어야 합니다.v와 s가 전단사bijective를 만족하면, set l v는 두 번, 세 번 반복해도 한 번 한 것과 같습니다.로 해석할 수 있습니다.
정보를 보존하며 변환할 때, injective인지, surjective인지는 중요한 속성을 가리킵니다.
v->s가 injective이면 적어도v의 구조는s에서 보존되었다는 말로,v에서 출발해서s로 갔다가v로 돌아 올 수 있다는 말은, s는 적어도 v이상의 정보량을 가지고 있다는 의미를 포함합니다.
v->s가 surjective라면,s에 있는 모든 것은v에 대응하는 대상이 있습니다. (하나가 아닐지라도요.s에서v로는 매핑 경로가 여러 개가 나올 수 있습니다.) v는 적어도 s이상의 정보량을 가지고 있다는 말입니다.
bijective하다면, 같은 양의 정보를 가지고 있다는 말을 포함하고 있습니다.x >= y,y <= x를 둘 다 만족하려면x = y인 경우만 있습니다.Q. 그냥
view,set이 bijective한 동작을 해야 한다, 혹은v,s는 bijective라고 쓰면 안될까?
A. 같은 내용을 코드로 표현한 것입니다. 저 코드 모양이 만족하는지 검사하는 건, GHC 컴파일러가 아니고 프로그래머 몫입니다.
Fri Dec 22 04:32:17 PM KST 2023 @todo 작성 중…
카테고리 이론에서 무언가가 닮았는지 보는 방법
1단계 - 두 카테고리가 얼마나 닮았나 보려면, 두 카테고리 사이의 펑터를 보고
2단계 - 두 펑터가 얼마나 닮았나 보려면, 두 펑터 사이의 자연 변환을 봅니다.
3단계 - 그럼 자연 변환이 얼마나 닮았나 보려면?
자연 변환의 각 성분들을 살펴 봅니다. 혹은 펑터 자체를 대상으로 하는 펑터 카테고리로 보면, 다시 1단계로 돌아갑니다. 그럼 자연 변환은, 대상 사이의 모피즘이 됩니다.
↦ 세로바가 앞에 붙은 화살표
Maplet이라 부르고, 예상하듯 함수를 뜻한다고 합니다. 매핑을 뜻하긴 하나, x ↦ f (x) 이렇게 쓰면, 람다 함수 \x -> f x와 같은 의미입니다. 그래서 홈펑터를 다음처럼 표기하기도 합니다.
hom(A,-): C -> Set
hom(A,-): B ↦ hom(A,B)모피즘 f: B->C 매핑은
hom(A,f): hom(A,B) -> hom(A,C)
hom(A,f): g ↦ f∘glocally small category
임의의 두 대상 사이의 모피즘 모음이 집합인 카테고리를 말합니다. 모음이 집합이 아닌 예로, 모든 집합 모음이 있습니다. 이 모음은 집합이 될 수 없습니다. 모든 집합의 모음이라 했으니까요. (러셀 역설) 그럼 locally small이 아닌 경우는 어떤 특징이 있는지 궁금하긴 한데, 일단 가던 길부터 잘 가고 생각해 봐야겠습니다. 텍스트들을 읽다 locally small을 만나면, 일단 “두 대상 사이에 모피즘 집합이 있군” 정도로 넘어 가려 합니다.
자연 변환 Natrual Transformation 표기
카테고리 C, D, 펑터 F: C -> D, G: C-> D 일 때, 자연 변환 η: F -> G …
이렇게 얘기하는 걸 다음과 같이 표기합니다.
[C,D](F,G)어떤 카테고리를 도메인, 코도메인으로 하고 있는지를 먼저 표시해 줍니다.
※ 아래는 C->Set 펑터를 나타냅니다. (역시나 펑터들이 대상이 되면, 모피즘과 혼동되지 않는 표기가 필요했을 거라 추측합니다.)
[C,Set] 또는 Set^C텍스트마다 다 다르긴 한데, 대체적으로
영문 소문자는 대상a, 혹은 모피즘f들을 표시하고,
영문 대문자는 카테고리C, 혹은 펑터F들을 표시하고,
(둘 중 하나를 볼드 한다든지, 필기체를 쓴다든지, 구별되는 표시를 하는 경우도 많습니다.)
그리스 알파벳 소문자는 자연 변환η을 표시합니다.
Aα 알파, Bβ 베타,γ 감마,δ 델타, Eϵ 입실론, Hη 에타, θ 세타, Mμ 뮤, Nν 뉴, ξ 크시, Pρ 로, Sσ 시그마, Tτ 타우, ϕ 피, ψ 프시, ω 오메가…
Hη는 homomorphism, Mμ는 monad 처럼 연결 고리가 연상되는 것도 있지만, 딱히 그런 것 없이 쓰는 경우가 많은 것 같습니다.
추측 - F를 적용한 결과와 G를 적용한 결과는 둘단 C의 구조를 보존한 상태기 때문에 자연스럽게Natrually 변환이 존재한다인가 봅니다.