Korean | English
대상: 처음 입문하는 분들이 볼 수 있는 안내서로 만들려 했는데, 몇 몇 부분에서 사전 지식이 좀 필요한 곳들이 있습니다. 아무래도, 하스켈 공부를 시작하고, 모나드, Arrow 문서들까지 봤는데, 찜찜함이 남은 분들이 봐야 적당할 것 같습니다.
저는 함수형 프로그래밍(이하 함수형)으로 돈을 벌고(벌려고 하고) 있으니 프로페셔널이라고 할 수도 있지만, 함수형의 기반을 공부하는 건 취미(아마추어)에 가깝습니다. 아주 밑바닥의 기반 지식이 없어도 함수형을 하는데 문제가 있는 건 아닙니다만, 그저 개인적인 성향으로 궁금한 것들이 있어, 여기 저기 뒤지고 다니며, 상상하고, 정리하고 있습니다. 아는 동료들이 거의 없어 지식이 맞는지 검증할 방법이 마땅치 않습니다. 정식 교육을 통해 익힌 지식들이 아니라 검증되지 않은 제 상상이니 주의하며 보시기 바랍니다.
이 글은 순수 함수에서 출발해서 함수형 입문에 필요한 용어, 개념들을 살펴보는 문서입니다.
함수형 프로그래밍을 공부할 때 난제의 시작은 순수 함수입니다.
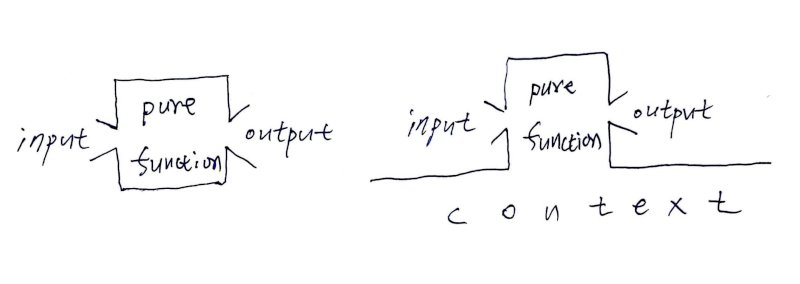
함수형 프로그래밍(이하 그냥 함수형)에서 함수는, 같은 입력으로 오늘 결과를 뽑든, 내일 결과를 뽑든, 몇 번을 실행하든 결과값은 달라지지 않습니다. 전역 변수나, 주변 어떤 상황에도 의존하지 않고, 오로지 입력에만 의존합니다. 언제든 입력을 안다면, 출력을 알 수 있어 참조 투명Referential Transparency하다라고 합니다.
※ 완전한 학술적 정의는 아니지만, 대충 입력, 출력에 명시되지 않고 함수 동작에 영향을 미치는 모든 요소를 Effect라 부릅니다.
과연 이런 제약을 지키고 프로그래밍이 가능할까 싶은, 너무 빡빡한 제약처럼 느껴집니다. Effect 없이 어떻게 실용적인 프로그램이 나올 수 있을까요? 실용 프로그램은 여러 상황에서 IO를 빼놓을 수 없으니 현실에서 쓰이는 프로그램을 만들려면 Effect는 반드시 필요합니다. (물론, 프로그램의 일부로 쓰일 라이브러리는 Effect가 없는 것들도 있을 수 있겠습니다만, 결국 결과를 눈으로 봐야한다면, 완성된 프로그램인데 Effect가 없을 순 없습니다.)
여러 교재들에서, 혹은 함수형 홍보 문구에선, 함수형은 Effect가 없다고 말을 합니다. Effect 없이는 실용적인 프로그램을 만들지 못하는데, 무슨 말일까요? 컴파일된 바이너리까지 확장해서 생각하면 Effect가 없는 설계를 한다기 보다 Effect를 잘 분리하는 게 목적입니다. 분리를 잘해서 힘 닿는데까지 순수하게 처리하고(순수한 척 하고), 잘 분리된 비순수 부분은 런타임에게 넘겨버리면 됩니다. 프로그래머 입장에서 비순수 부분을 만나지 않는다면, 함수형은 순수하다고 말할 수 있겠습니다.
참조 투명성을 지키면 무슨 좋은 일이 생겨, 이리도 빡빡한 기반을 만들고 시작했을까요?
※ Effect가 없는 함수를 순수 함수라 하고, Effect가 있는 함수는 액션Action이라고 부르거나, 아예 함수란 이름 대신 프로시저Procedure라 부르기도 합니다.
간단한 절차형 의사코드를 보겠습니다.
funcPlus v
return v + v * global
funcMinus v
return v - v * global
main
global = 1.1
init = 1
res = funcPlus init
res = funcMinus res
print res funcPlus와 funcMinus에서 필요한 정보를 매개 변수로 모두 받지 않고, global 변수에 두고 접근하고 있습니다. 이 함수들은 입력으로 들어오지 않은 global에 의존하고 있습니다. 참조 투명하지 않고, 순수 함수가 아니고, Effect가 있으며, 액션이라고 부릅니다.
함수형에선 전역 변수를 둘 수 없습니다. 필요한 정보는 모두 매개 변수로 받아야 합니다.
funcPlus gparam v
return v + v * gparam
funcMinus gparam v
return v - v * gparam
main
global = 1.1
init = 0
res = funcPlus global init
res = funcMinus global res
print res 그리고, 함수형에선 변수에 대입해서 기억하는 방법이 존재하지 않습니다. 위와 같이 res에 대입해서 기억시킬 수 없습니다.
main
print (funcMinus 1.1 (funcPlus 1.1 0))위와 같이 함수 하나가 끝나면, 결과를 다음 함수가 바로 받아야 합니다.
데이터에 어떤 작업을 하고, 변경된 데이터를 다음 작업이 받아 작업하고, 변경된 데이터를 또 다음 함수에 넘기고…
이렇게 보일 수 있지만, 초기값을 넣어 주기 전에, 즉 값이 아직 없는 상황을 보면,
\init global -> print (funcMinus global (funcPlus global init))비어 있는 정보가 잘 보이게 써 보면,
\_ _ -> print (funcMinus _ (funcPlus _ _))함수들을 먼저 묶어Combine 길을 만들고 있습니다. 전역 변수를 쓰던 코드를, 별 거 아닌 것처럼 보이지만 거창하게도
Effect가 필요한 상황을 순수 함수만으로 모델링 했습니다.
튜링 머신에선 상태가 있는데, 람다 산법에는 상태를 둘 데가 없습니다. 그런데, 어떻게 튜링 머신이 할 수 있는 일을 모두 람다 산법으로 할 수 있을까요? 정말 번거로워 보이지만, 위 예시처럼 모두 매개 변수로 받으면 됩니다. 하지만, 딱 봐도, 매 번 global을 넘기면서 프로그래밍하는 건 여간 번거로운 일이 아닌 게 보입니다. 계속 의존하는 정보가 늘어날 수록, 이론상은 가능할지 몰라도, 현실적으론 불가능에 가깝습니다.
람다 산법이 아니라, 프로그래밍쪽에선 람다 함수를 별 다른 설명 없이, 그냥 이름 없는 함수라 하고 넘어가는 문서들도 가끔 만납니다. 이름이 없으니, 나중에 다른 곳에서 못 부르는 함수겠거니 하고 넘어가는데, 쓰임새를 보면 꼭 짚고 넘어가야 하는 성질들이 있습니다.
다음 처럼 x를 받으면, 값이 아니라 함수를 반환하도록 할 수 있습니다.
\x -> (\y -> doSomething x y)x를 주면, 결과로 반환하는 함수인 \y->... 함수에서만 보면, 분명 입력으로 들어 오지 않은 x를 참조하고 있습니다. Effect가 없는 순수 함수여야 하는데, 이렇게 보면 순수하지 않은 듯 보일 수 있습니다. \y->... 함수를 얻으려면, 반드시 x를 넣어 줘야만 합니다. x가 들어 온 후에 받은 \y->... 함수 입장에서 x는 (캡처된) 상수입니다. 모양은 입력으로 들어 오지 않은 정보를 접근하는 것 같지만, \y->... 함수 안의 x는 외부 정보가 아니라, 이미 고정된(컨텍스트의 캡처된 값에 바인딩된) 값을 가지고 있습니다. (함수 코드 덩어리를 수정하진 않고, 어딘가Context에 x를 기억해(캡처해) 두고 필요할 때 가져옵니다. 컨텍스트와 컨텍스트를 참조하는 함수를 합쳐 클로저라 부릅니다. \y ->...에서만 보면 x는 어떤 람다 헤드에도 묶이지binded 않아 자유Free 변수라고 부릅니다.)
모두 순수 하지만, 순수하지 않은 듯이 보이는 이 동작이, 바로 리얼 월드의 순수하지 않은 일을 해결할 힌트입니다!
※ 람다 산법에서 자유 변수가 없는 람다 함수를 컴비네이터라 부르는데, 하스켈 교재들을 읽을 때는, 이름 그대로 함수나 어떤 타입의 값을 조립Combine할 수 있게 해 주는 함수를 컴비네이터라 부른다고 보는 게 편합니다. (자유 변수가 없으면, 컨텍스트와 상관 없이 독립되어 있기 때문에 “조립” 요소로 볼 수 있으니, 결국 같은 뜻처럼 보이기도 합니다.)
※ Combinatory logic 참고
\v gparam -> v + v * gparam -- (가)
\v gparam -> v - v * gparam -- (나)이 렇게 두 함수를 정의하고, 두 함수를 조립하기 위해, 아래와 같은 컴비네이터를 정의해 보겠습니다.
\f g -> \v -> g (f v) -- 늘 보던 함수 합성입니다.※ 위와 같은 컴비네이터로 f와 g를 합성할 수 있다면, f와 g도 역시 컴비네이터라 부릅니다.
이렇게만 정의하면, gparam을 넘길 방법이 없으니, g, f에 gparam을 넘겨 주게 하고,
\f g -> \v -> g gparam (f gparam v)이제 자유 변수인 gparam을 람다 헤드에 걸어 주면,
\gparam -> \f g -> \v -> g gparam (f gparam v)마치 \gparam이 전역 변수 역할과 비슷해 보이지 않나요? \gparam -> 아래에 있는 함수 f와 g는 gparam에 접근 가능합니다. gparam 값을 넣어 주면, 두 함수를 합성하며, 각 각의 함수에 gparam을 넣어 적용할 준비를 마친 \f g ->... 함수를 반환합니다. 이 함수에 (가)와 (나)를 넣어주면 원하는 동작을 할 수 있습니다. gparam을 가진 함수들을 조립할 수 있는 새로운 컴비네이터를 정의해서 이들을 조립(합성)할 수 있게 됐습니다.
전역 변수 없이, 참조 투명성을 지키며 원하는 동작을 하게는 만들었지만, gparam이 점점 늘어가면 계속 이런 방식으로 이어 나가기가 힘들거란 걸 어렵지 않게 예상할 수 있습니다.
이제 gparam을 계속 넘기는 건 변함없지만, 신경쓰지 않게 만들어 보겠습니다.
대상을 바라보는 눈을 바꿔서 funcPlus와 funcMinus가 값을 반환하는 것이 아니라, gparam을 받으면 값이 될 함수, 즉 gparam을 받기 전에 할 수 있는 일은 모두 해 놓고, gparam을 받으면, 그 때서야 값이 되는 함수까지만 만들어 반환 하도록 바꿔 보겠습니다.
\v -> \gparam -> v + v * gparam -- (다)
\v -> \gparam -> v - v * gparam -- (라)v를 넣어도, 값을 만들어reduce 반환하는 것이 아니라, gparam을 받아야 값이 되는 함수를 반환합니다.
이제 이 둘을 조립하는 컴비네이터를 정의해 보겠습니다.
\f g -> (\initV -> (\gparam -> g ((f initV) gparam) gparam))조금 복잡해 보이지만, f의 결과에 gparam을 적용해서 g에 넘기고, 이렇게 해서 만들어진 함수에 또 gparam을 적용하고 있습니다.
위에 정의했던 컴비네이터와 거의 비슷하지만, 다음과 같은 차이가 있습니다.
-- \gparam -> (\f g -> (\initV -> g gparam (f gparam initV)))
\f g -> (\initV -> (\gparam -> g (f initV gparam) gparam)) -- (마)인자를 받는 순서만 바꾸어 놓은 모양이고, 결과는 같습니다. f, g, initV를 받았다면, 마지막으로 gparam을 받아야만 값이 되는 상황입니다.
둘이 비슷해 보이지만 좀 다릅니다. 함수에게 일부 인자만 넘겨서, 일부 인자는 고정된 상태로 보는 게 Partial application이고, 커링은 고차 함수가 지원될 때, 함수가 하나의 인자만 받고, 나머지 인자를 받아야 하는 함수로 반환하도록 만드는 걸 말합니다.
\x y -> x + y를 커링하면,
\x -> (y -> x + y)\y -> x + y 함수를 손에 쥐려면, \x로 값을 넣어 줘야 얻을 수 있으니, 만일 손에 이 함수를 들고 있다면, 이 함수는 x를 알고 있다는 얘기입니다. 컨텍스트에 x값이 들어 있다고 말합니다.
타입은 컴파일러와 대화하기 위한 “언어” 역할을 합니다. 타입 레벨 프로그래밍까지 넘보려면 꽤 복잡한 성질들을 알아야 합니다. 당연히 전반적인(포멀한) 타입 설명을 하려는 건 아닙니다. 여기서는, 잘 말하지 않는 한 가지 성질만 보겠습니다.
타입은 나중에 할 일을 표기하는 방법 중 하나로 볼 수 있습니다.(아직 같은 방식으로 얘기하는 문서는 못봤습니다. 저 혼자만의 상상입니다.) 뭔가 작업을 해야 하지만, 지금은 이름만 붙이고 넘어가고, 필요한 때가 오면 실행할 수 있는 장치 역할을 할 수 있습니다.
initV를 넣어 주면 나중에 gparam을 받아야만 값이 되는 함수들 (다)와 (라)를(마)컴비네이터를 써서 합성하면,initV를 받아서 값을 돌려주는 게 아니라, gparam을 받아야만 되는 함수를 결과값으로 돌려 주고 있습니다.gparam을 받는 부분을 타입으로 감싸 놓고, 타입 안의 값이 필요하다면 반드시 gparam을 넣어야만 되도록 만듭니다.
하스켈로 표현하면 다음 정도 되지만,
data RequireG a = { runner :: gparam -> a }지금은 그냥 gparam을 넘기면 값이 되는 타입을 RequireG이라 이름 붙였다고 생각하겠습니다. 그리고 언젠가 값이 필요하다면 gparam을 넣어 주는 runner를 돌리면 됩니다.
f :: RequireG a
g :: RequireG a
(마) :: RequireG a -> RequireG a -> RequireG a컴비네이션! 만일 RequireG 함수가 몇 십 개, 몇 백 개가 있어도, 이들을 모두 (마)로 합성하면, 수면 밑에서는 엄청나게 많은 절차가 있더라도, 수면 위만 보면 하나의 RequireG 타입의 함수일 뿐입니다. RequireG 타입의 컴비네이션을 하나의 값처럼 쓰다가, 최종 값이 필요할 때가 되면, runner로 전역 변수 역할을 하는 값을 넣어주면 됩니다.
조각을 조립한 전체를 보면 순수하지만, 특정 조각의 입장에서 보면 비순수
이제, 최종 주제로 들어갈 준비가 된 것 같습니다. 지금까지 이 부분을 얘기하기 위한 용어들을 간단하게 짚어 봤습니다. 이제 함수들을 조립하는 동안, 각 함수들의 결과들을 어떻게 상태(처럼)로 다룰 수 있는가를 살펴 보겠습니다.
상태가 없는 함수형에서 상태를 대신할 매커니즘이 필요합니다. 하스켈을 공부하면서 만나는 주제들 중, 입문자에게 난이도 높은 걸로 악명을 떨치는 것들이 이 것과 관련이 있는 것들이 많습니다. 순수 함수로 비순수한 작업을 “효과적으로 모델링”할 방법이 필요합니다.
funcPlus gparam v
return v + v * gparam
funcMinus gparam v
return v - v * gparam
main
global = 1.1
init = 0
res1 = funcPlus global init -- f1
res2 = funcMinus global res1 -- f2
res3 = res1 + res2 -- 각 각 함수의 결과에 따로 접근 합니다.
print res3 res3 부분처럼 기존 묶었던 함수들의 각 각의 결과가 필요한 경우를 보겠습니다. 이 게 해결되지 않으면 실용 프로그램을 만들기가 정말 까다로워집니다.
함수형에선 변수가 없다고 하는데, 좀 삐딱하게 얘기하면 아닙니다. 한 가지 방법이 있습니다. 바로 람다 헤드에 걸어 두면 됩니다.
\init global -> print (funcMinus global (funcPlus global init))위에서 값을 바로 다음 함수에 넣어주던 모양을, 각 함수의 결과를 람다 헤드에 걸어 보겠습니다.
\init -> (\res1 -> (\res2 -> (print res1 + res2)) (funcMinus global res1)) (funcPlus global init))보기 복잡하니 일단 f1, f2 로 바꿔 보겠습니다.
-- ___________________________________________
\init -> (\res1 -> (\res2 -> res1 + res2) (f2 res1)) (f1 init)
-- ^^^^^^^^^^^^^^^^^^^^^^
-- 여기서 res1에 접근 할 수 있는 걸 주목해 주세요.여전히 복잡해 보입니다. 값에 함수를 적용하는 컴비네이터를 정의해 조금 더 보기 좋게 표현을 바꿔 보겠습니다.
(>>>>>) v f = f v중위 연산자로 인자 두 개 사이에 연산자로 둘 수 있습니다. v >>>>> f로 쓸 수 있습니다.
\init -> (f1 init) >>>>> (\res1 -> (f2 res1) >>>>> (\res2 -> res1 + res2))(>>>>>)의 연산의 우선 순위를 오른쪽 결합으로 하면, 아래처럼 괄호를 생략할 수 있습니다.
\init -> (f1 init) >>>>> \res1 -> (f2 res1) >>>>> (\res2 -> res1 + res2)함수 적용이 >>>>>보다 우선 순위가 높다고 두면, (람다 함수 정의 끝은 표현식 끝까지입니다.)
\init -> f1 init >>>>> \res1 -> f2 res1 >>>>> \res2 -> res1 + res2하스켈은 슈거 문법으로 do를 정의해 두었습니다. 비슷하게 >>>>>와 \res ->의 슈거 문법 dolike를 정의해서 아래처럼 보이게 할 수 있습니다.
job init = dolike
res1 <- f1 init
res2 <- f2 res1
return res1 + res2각 함수들의 결과값에 따로 접근 가능한 상태로 컴비네이션을 만들 수 있게 되었고, 보기도 나쁘지 않습니다.
이 방식이 모나드 바인드가 쓰는 방식입니다. (모나드의 목적이란 말이 아니라, 모나드의 바인드가 액션의 개별 결과를 저장하는 방식을 말하고 있습니다. 모나드의 목적은 Effect들을 다루는 것으로, 여기서는 Effect를 다루기 위한 동작 중 일부만 얘기하고 있습니다.) 하스켈에 do 표기법 포함 모나드를 도입한 사람은 필립 와들러 교수라 합니다. 어찌 이런 걸 생각해 냈을까요? 너무 익숙한 모양과 딱 맞아 떨어지니 감탄스럽습니다.
(※ 처음 프로그래밍 이론에 모나드를 도입한 사람은 유지니오 모기 교수입니다.)
@todo 위에 살펴본 개념들을 모두 적용해서, 어떻게 gparam(Effect가 있는)을 받는 액션들을 조립combine하는지 보이려고 합니다만, 아직 정리가 덜 됐습니다. (2024.11)
클로저 말고, 더 명시적으로 데이터를 끌고 다니는 컴비네이터를 설계할 수도 있습니다.
몇 개의 함수를 컴바인할지 몰라, 결과값도 몇 개를 기억하고 있어야 할지 정해져 있지 않은 경우를 생각해 보겠습니다. 데이터 수량이 정해지지 않은 경우를 표현하기 위한 방법이 뭐가 있을까요?
가장 먼저 떠오르는 걸로는 재귀 데이터 타입인 리스트가 있습니다.
data List a = Null | Cons a (List a)재귀 데이터 타입으로 리스트가 가장 만만해 보였는데(리스트로 해결해도 되지만), 더 만만한 타입이 있습니다.
2튜플을 살펴 보겠습니다. 튜플 자체는 재귀 데이터 타입은 아니고, 튜플속에 튜플을 넣는 모양으로 중첩 구조를 만들 수 있습니다. (꼭 튜플이 아니더라도 중첩을 만들 수 있는 구조면 뭐든 상관없지만, 이미 있는 것들 중 가장 간단한 구조는 튜플입니다.)
a를 입력으로 주면 f a와, 이어지는 g a의 결과값을 모두 유지하려면,a를 2튜플로 만듭니다. (a,a)f를 적용합니다. (f a, a)g를 적용합니다. (f a, g a)h가 이어진다면 (f a, (g a, h a))로 만듭니다.이 방식이 Arrow가 사용하는 방식입니다.
여러 천재들의 손을 거쳐 찾은 해결책들을, 바닥부터 아카데믹하게 이해하는 게 아니라, 실전 하스켈 코드를 보고 수긍할 정도의 눈을 갖는 게 목표입니다.
여기서는 모나드와 Arrow 전체를 보려는 것이 아니라, 순수 함수로 인해 생긴 문제를 둘은 어떻게 해결하나 살펴 봤습니다. 전 이렇게 보는 게, 컴비네이터들이 왜 그렇게 생겨 먹은 건지 이해하는데 조금은 도움이 됐습니다. 난해한 컴비네이터를 만나 이해가 어려울 때, 위와 같은 동작을 하는 부분은 없나 살펴 보며 접근해 보는 것도 나쁘지 않겠습니다.
아직 최종 목적지에 도달하지 못해, 용두사미 같은 글이지만 미리 오픈합니다. 콕 집어서 이런 내용으로 정리한 글이 없어, 어디가 틀렸는지, 관심 있는 분들과 대화가 열렸으면 좋겠습니다. (분명 절차형만 다루던 엔지니어가 부드럽게 들어갈 길이 있을 것이라 믿고, 혼자 뒤지는 중입니다.)